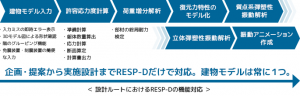
前回の記事ではファイバーモデルのメリット、デメリット、材端剛塑性ばねモデルとの違いなど、ファイバーモデルの概要について説明しました。今回は、ファイバーモデルにおける断面解析の流れを簡単に紹介したいと思います。
目次
1. ファイバーモデル紹介
はじめにファイバーモデルの概要を説明したいと思います。ファイバーモデルは、断面が複数の微小断面(セグメント)により分割されたモデルであり、それぞれのセグメントが独立した応力ひずみ関係を持っています。概要を下図にまとめています。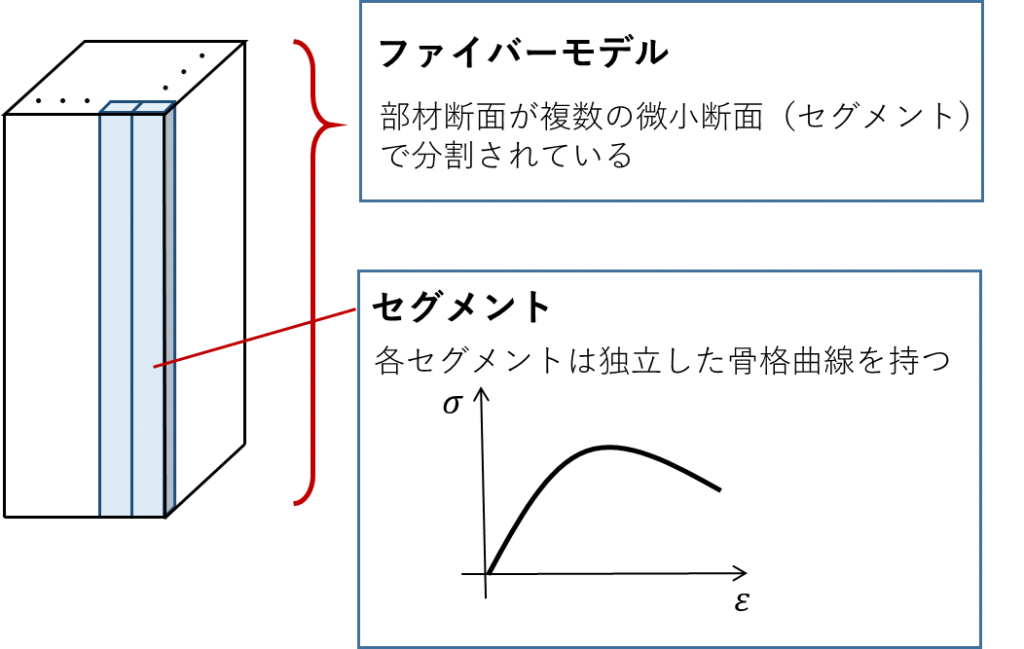
- 微小変形を仮定する。
- 塑性化領域は1つ(要素全体)とする。
- 曲げモーメントと軸力のみ考慮する。(せん断力は考慮しない)
2. ファイバーモデルに対する断面解析
2.1 計算フロー
ファイバーモデルに対する弾塑性断面解析の計算の流れを下図に示しました。外力を増分させ、各ステップごとに構造部材の応力、ひずみを評価し、要素の剛性を更新していきます。
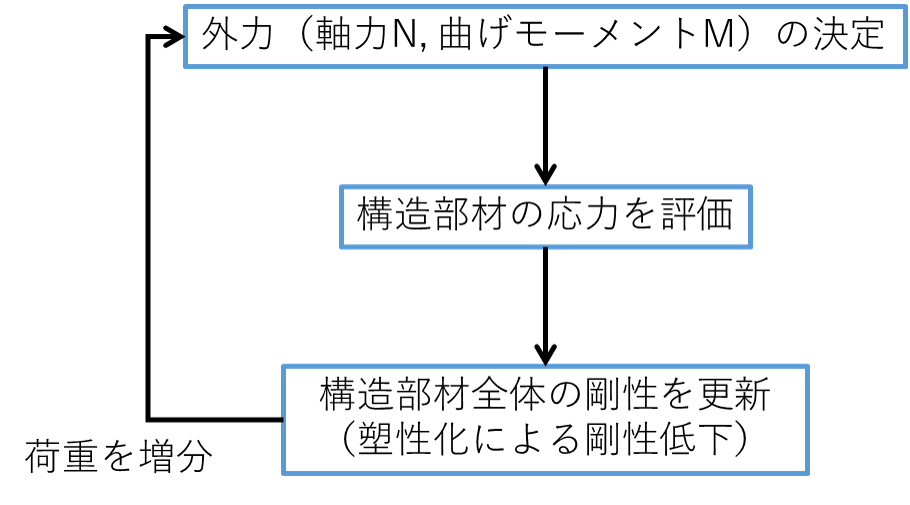
ファイバーモデルでは、上図の「構造部材全体の剛性を更新」にて特徴的な計算が必要になります。この剛性の更新方法について次節から詳しく紹介します。
2.2 要素剛性の更新方法
2.2.1 剛性更新フロー
ファイバーモデルに注目した剛性更新の流れを下図に示しました。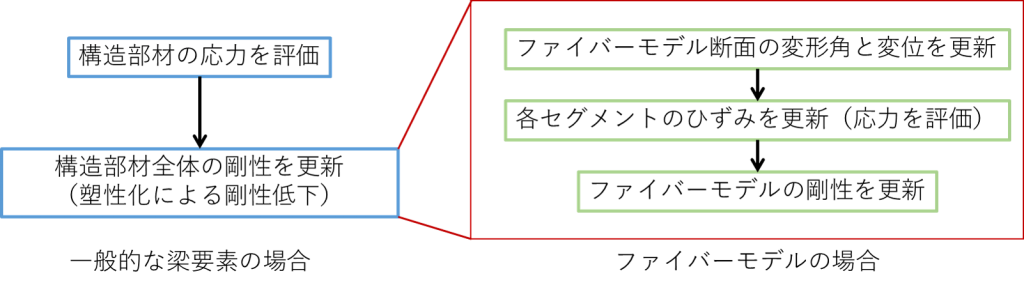
- 平面保持仮定を適用しファイバーモデル断面の曲率とひずみを計算
- 各セグメントの剛性を更新
- ファイバーモデル全体の剛性(軸剛性、曲げ剛性)を更新
2.2.2 両端断面の曲率とひずみ
ファイバーモデル断面の図を下図に示しました。平面保持仮定が成立しているとすると変形前に対する変形後の断面の位置関係は下図のようになります。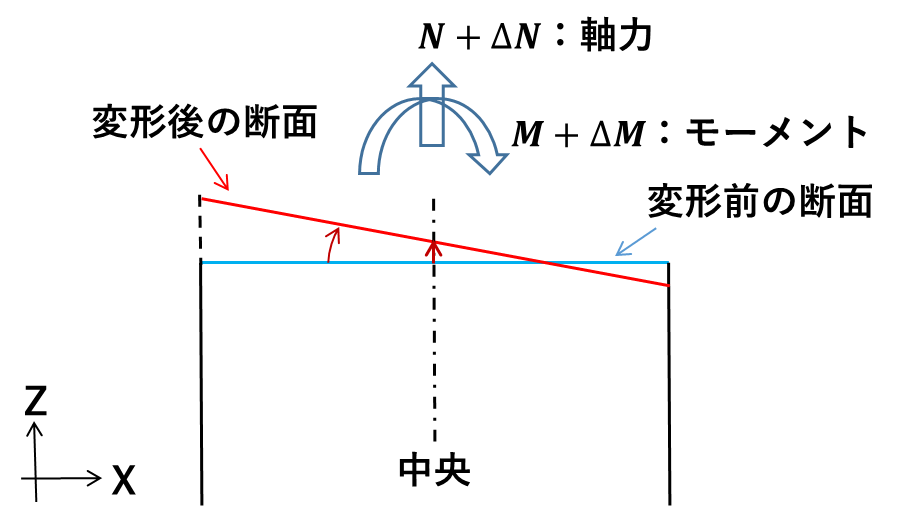
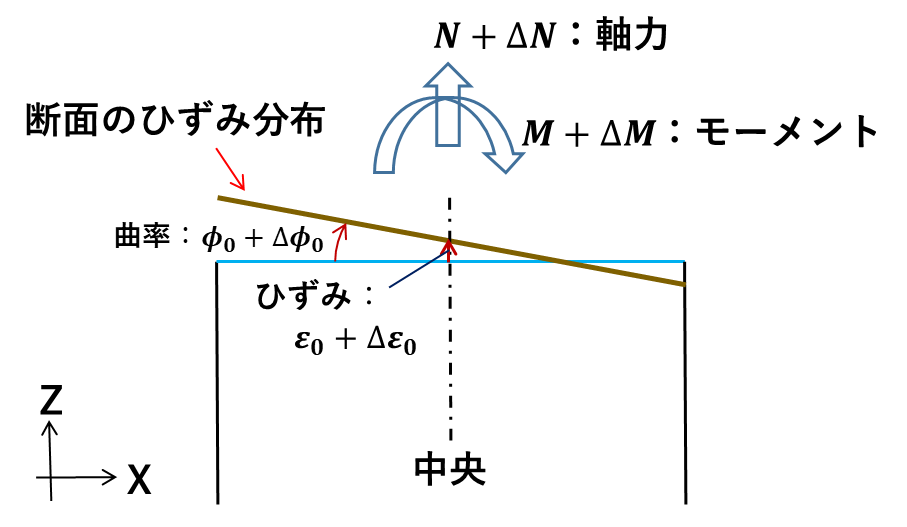
三次元の場合はX軸回りの曲率も加わります。
2.2.3 各セグメントの剛性を更新
2.2.2節で断面の曲率 、中央位置のひずみを求めることができました。部材断面の形状は変形後も平面を保つとする仮定(平面保持仮定)を適用することで、各セグメントのひずみを算出することができます。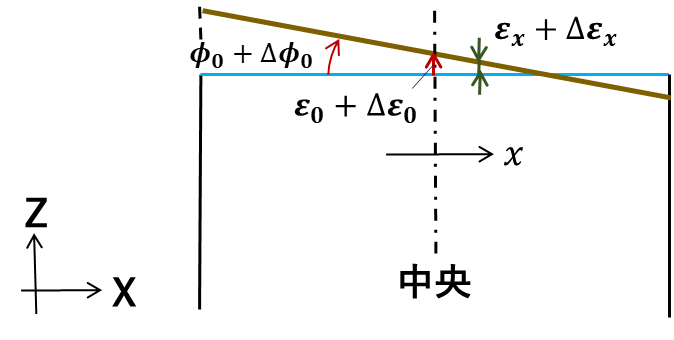
$$\large \Delta \varepsilon (x) = \Delta \varepsilon_0 - x \cdot \Delta \phi_0$$
と表せます。
各セグメントのひずみが分かると、各セグメントの剛性を求めることができます。セグメントが下図のような骨格曲線を持っているとすると、
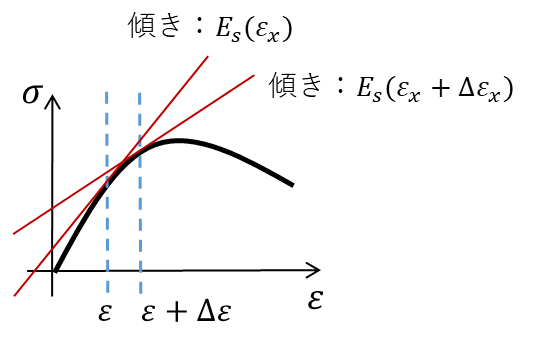
各セグメントの剛性は \(E_s(\varepsilon_x)\) から\(E_s(\varepsilon_x + \Delta \varepsilon_x) \) に更新されます。
2.2.4 ファイバーモデル全体の剛性を更新
2.2.3節で各セグメントの剛性を更新することができました。最後に各セグメントのひずみから、ファイバーモデル全体の剛性を求めます。 まず下図のようなファイバーモデル断面を想定します。セグメント1つ分の断面積を\(A_s\)、図心から各セグメント中央までの距離を\(y_s\)) と定義します。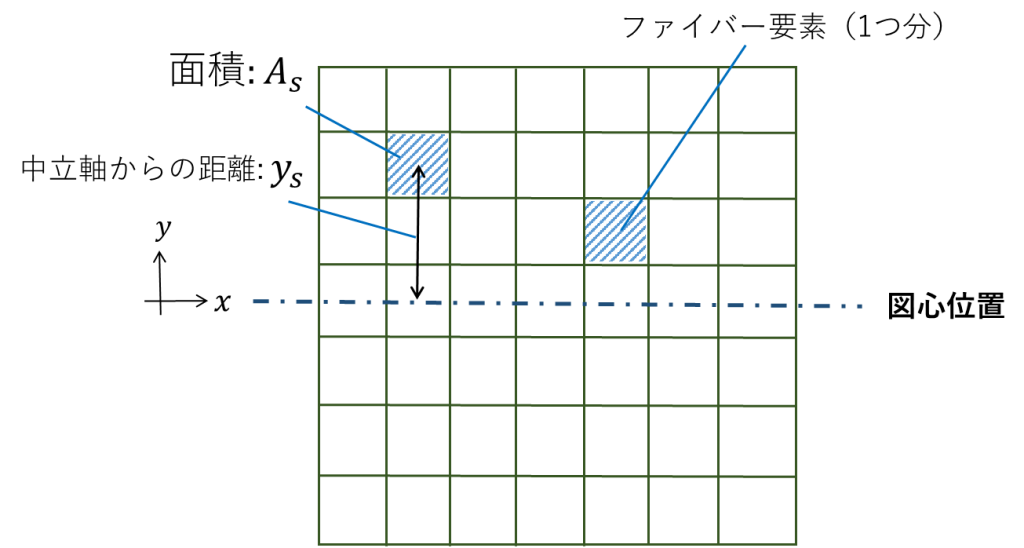
ファイバーモデルの断面
$$\large EA = \sum E_s \cdot A_s$$
と求められます。一方で曲げ剛性EIは、剛性の変化による中立軸の移動を考慮して、
$$\large EI = \sum E_s \cdot A_s \cdot (y_s-y_0)^2$$
と表されます。 ここで\(y_0\)は中立軸の移動量を表しており、下式のように計算できます。
$$\large y_0= \frac{\sum E_s \cdot y_s \cdot A_s}{\sum E_s \cdot A_s}$$
以上より、ファイバーモデル全体の軸剛性、曲げ剛性を算出(更新)することができました。荷重を増分し、新しい剛性でひずみを評価し、、と繰り返すことでファイバーモデルに対して弾塑性の断面解析を実行することができます。
前回の記事(ファイバーモデル入門)でご紹介したように、本来は塑性化領域と弾性領域で分けてモデル化することもできます。そのような場合は、内点(両端部ではない部材内部にできる節点)の情報を消去(マトリックスの縮約)する必要がありますが、応用的な内容のためここでは割愛します。
3. 考察
最後に、ファイバーモデルの剛性更新の際に考慮した「中立軸の移動」と、ファイバーモデル計算方法の課題である「平面保持仮定の成立性」について考えてみたいと思います。3.1 中立軸の移動とは
「中立軸の移動を考慮する」とはどういうことでしょう。弾性範囲では、中立軸位置は図心位置と等しいとして扱います。 では、そもそも中立軸位置と図心位置はなぜ等しいとして扱えるのでしょうか。 まず中立軸位置とは、「曲げモーメントのみを作用させたとき(純曲げ状態時)に軸ひずみが発生しない箇所」を表しています。この時、断面内の軸応力( \(\sigma\) )は平面保持仮定より、$$\large \sigma = E \cdot \frac{y}{\rho} $$
と表されます。 (断面内の剛性をE、曲率半径を\(\rho\)、中立軸からの距離を\(y_s\)) 純曲げ状態の時、断面内の軸力の合計は0なので
$$\int_A \sigma dA = 0$$
が成立します。断面内の剛性Eは一定だとすると、
$$\frac{E}{\rho} \cdot \int_A y dA = 0$$
すなわち、断面一次モーメント \(\int_A y dA\) が0となる位置(図心位置)が中立軸位置と一致することになります。 しかし、断面の一部が塑性化すると、剛性Eを積分の外に出せず、
$$\large \frac{1}{\rho} \cdot \int_A E \cdot y dA = 0$$
となりますので、図心と中立軸は一致しなくなります。つまり、中立軸が図心位置から移動してしまいます。 このような現象を考慮するために、中立軸位置を計算し直していました。RESP-F3T、RESP-Dでもそのような中立軸の移動を考慮した計算を行っています。
移動後の中立軸位置を\(y^*\)とすると
$$\large \frac{1}{\rho} \cdot \int_{A} E \cdot (y-y^*) dA = 0$$
が成立する\(y^*\)を求めればよいので、
$$\large y^* = \frac{\int_{A} E \cdot y dA}{\int_{A} E dA}$$
と求めることができます。
3.2 平面保持仮定は必ず成立するか
平面保持仮定は必ずしも成立するとは限りません。例えば以下の図に示したように、鉄筋コンクリート造柱の中で鉄筋とコンクリートの間にすべりが生じた場合、平面保持仮定は成立できなくなります。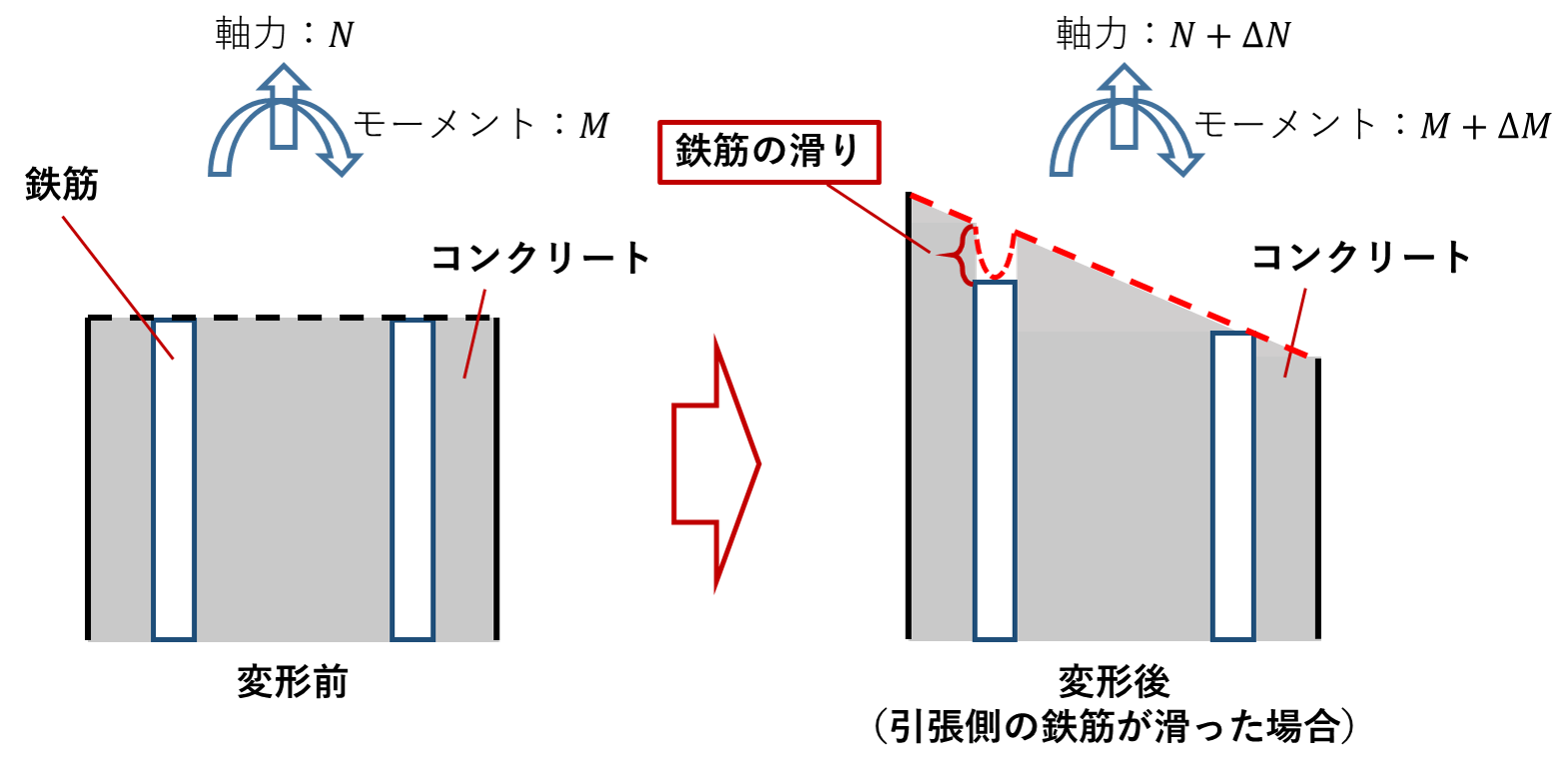
- 鉄筋の骨格曲線として、コンクリートとのすべりを模擬できるような多岐線を定義する。 (比較的簡易な方法だが、多岐線の定義方法が確立されていない。多岐線の求め方については弊社のメンバーが検討を進めています。[1] )
- セグメント間に摩擦ばねを配置する。[2](モデルが複雑となり、計算コストが大きいが、物理的に理解しやすい)
参考文献
[1] 鈴木, 梁川, 宇佐美, 木村, 履歴形状を考慮した材端剛塑性ばねモデルと適合するRC部材のファイバーモデル化 その1 両端固定梁要素による検討, 2018, 日本建築大会[2] Giorgio Monti and Enrico Spacone, "Reinforced Concrete Fiber Beam Element With Bond-Slip", 2000 June, JOURNAL OF STRUCTURAL ENGINEERING
まとめ
本記事ではファイバーモデルに対する断面解析の簡易な計算方法を紹介しました。計算の流れは大きく以下3ステップに分かれていました。1. ファイバーモデル端部断面の曲率・ひずみを計算
2. 平面保持仮定より各セグメントのひずみを算出後、剛性を更新
3. 各セグメントの剛性からファイバーモデル全体の剛性更新
次に、今回の計算方法に対する考察として、
・中立軸の移動
・平面保持仮定が成立性
を取り上げました。
中立軸の移動は、セグメントが降伏し剛性が低下することで発生する現象であり、弾塑性状態を考慮するためには逐次計算する必要があります。
一方で今回のファイバーモデル計算方法の弱点として平面保持仮定が成立しない場合を取り上げました。例として、鉄筋コンクリート内部の鉄筋の付着がはがれ、コンクリート内部で滑るような場合があります。そのような現象を詳細に取り扱う必要がある場合、今回の計算方法をそのまま適用することができません。簡単な対策としては、鉄筋に付着の滑りを考慮した骨格曲線を与える方法などが考えられますが、方法はまだ確立されていないことが現状です。
ファイバーモデルは計算方法が少し複雑ですが、構造力学による直接的な理解がしやすいモデル化方法だと思います。ぜひ、これを機にファイバーモデルの利用を検討してみてください。
プログラム紹介