粘弾性ダンパーの取り付け剛性と解析収束性の関係を複素剛性から考察する

粘弾性ダンパーを用いる際、取り付け剛性によっては収束しにくく時間刻みを細かくする必要があります。取り付け剛性によって粘弾性ダンパーを用いた解析が発散してしまう現象はよくあるお問い合わせの1つです。
本件については以前その現象を定性的に考察し、注意点などをまとめています。
粘弾性ダンパーを用いた振動解析の注意点

粘弾性ダンパーを用いた解析が発散しやすいのは、粘弾性ダンパーの減衰係数の接線勾配が小速度領域で大きく、前ステップによって計算された速度増分量$\Delta V$による次ステップの不釣り合い力が大きくなるためです。

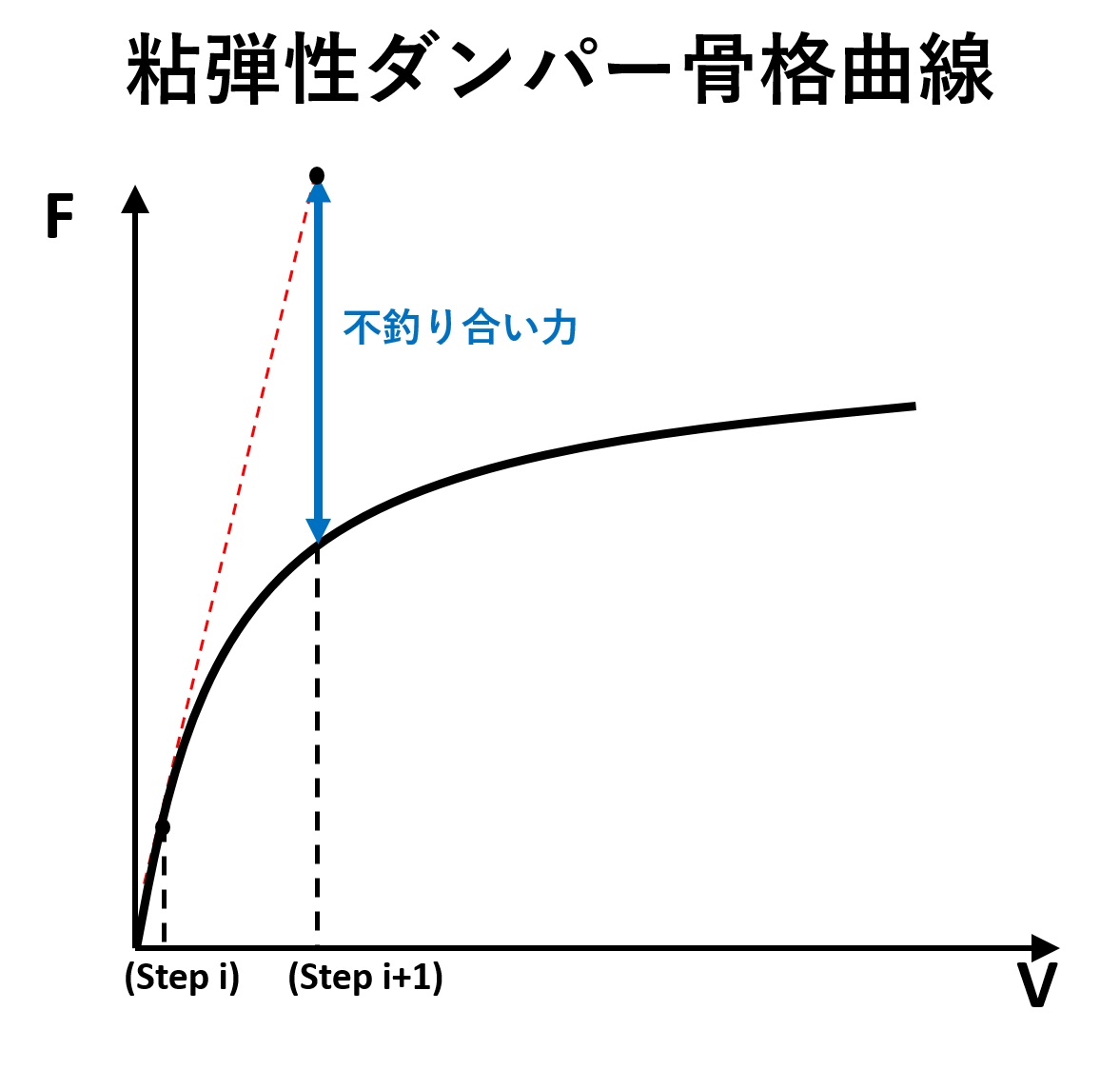
また適切な取付剛性による効果を下記のように説明しました。

適切な取付剛性を設定することで、下図に示すように計算が発散しやすい微小変形（速度）領域ではばねの挙動が支配的となります。つまり、減衰係数が非常に大きい微小変形領域（速度）においてダッシュポットに速度が発生しにくい状況になり、結果的に発散が生じにくくなります。

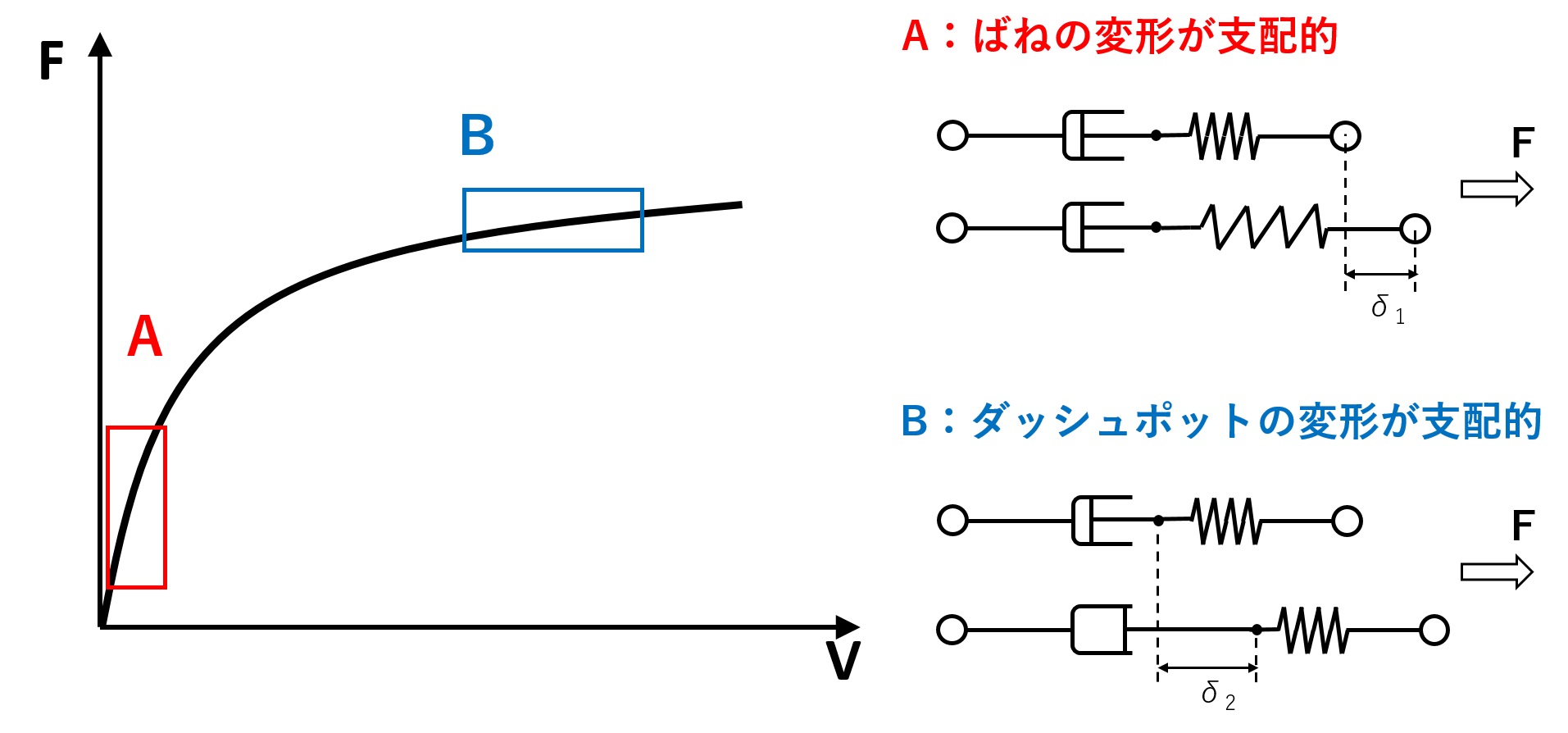
今回はこれらの

取り付け剛性とダッシュポッド・取り付けばねの挙動の関係
取り付け剛性と解析安定性の関係

を複素剛性を用いて解析的に考察したいと思います。

1. 複素剛性とは
2. 直列な減衰装置の場合（内部剛性がダッシュポッドに対して直列に取り付くモデルの場合）
2.1 取り付け剛性とダッシュポッド・取り付けばねの挙動の関係
2.2 取り付け剛性と解析安定性の関係
3. 並列な減衰装置の場合（内部剛性がダッシュポッドに対して並列に取り付くモデルの場合）
3.1 取り付け剛性とダッシュポッド・取り付けばねの挙動の関係
3.2 取り付け剛性と解析安定性の関係
3.2 取り付け剛性が有限でありかつ非常に大きな値の場合
まとめ

1. 複素剛性とは

複素剛性とは複素数で表す剛性の事です。複素数を用いることでダッシュポッドのような速度に依存する装置の抵抗力も「剛性」として表すことができます。これによりバネ同士の直列つなぎ、並列つなぎのように全体の剛性値を簡単に求めることができます。

例えば、下図のような減衰定数$c$をもつ粘弾性ダンパーの複素剛性$ K_c $の場合、
$ \alpha $、$ A $は実数の定数とし、$ j = \sqrt{-1} $とし、入力変位$ x $を
$$\large x = A \cdot e^{j \alpha t} $$

とおくと、ダッシュポッドの力を$F_c$は

$$\large F_c = c \cdot \dot{x} $$
と表されるため、
$$\large F_c = jc\alpha \cdot x $$
よって、ダッシュポッドの複素剛性$K_c$は
$$\large K_c = j c \alpha $$
と表せます。

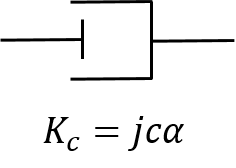
2. 直列な減衰装置の場合（内部剛性がダッシュポッドに対して直列に取り付くモデルの場合）

下図のような、ダッシュポッドに対して取り付け剛性が直接、直列に取り付く場合考えます。
（ダッシュポッドに直列な内部剛性がある場合も同様ですので、内部剛性は省略しています。）

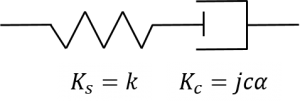
各々複素剛性を考えると、その合成された複素剛性$ K_{all} $は、

$$\large \frac{1}{K_{all}} = \frac{1}{K_s} + \frac{1}{K_c} $$
よって
$$\large K_{all} = \frac{k \cdot j c \alpha}{k+jc \alpha} $$
と導けます。

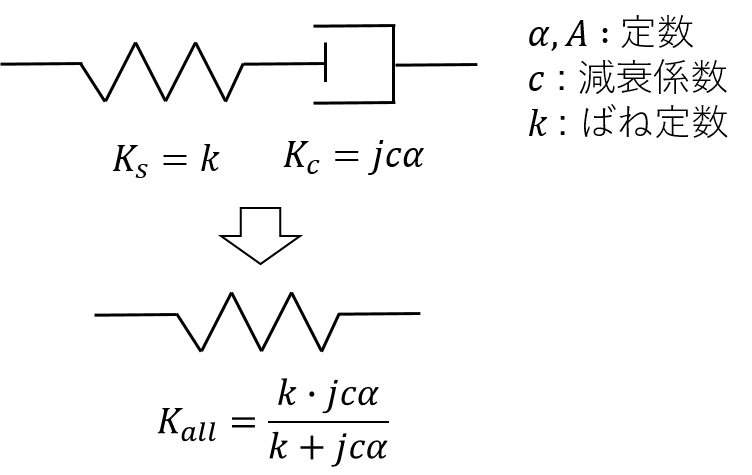
2.1 取り付け剛性とダッシュポッド・取り付けばねの挙動の関係

外力$\Delta F$による、減衰系全体の変位を$\Delta X$とすると、

$$ \large \Delta X = \Bigl(\frac{1}{k} + \frac{1}{jc\alpha}\Bigr) \cdot \ \Delta F $$

と導けます。$\frac{1}{k}$が取り付けばねによる変位、$\frac{1}{jc\alpha}$がダッシュポッドの変位に対応しています。

$k$が$|jc\alpha|$より十分大きい場合には、減衰系全体の変位に対してダッシュポッドの変位が支配的となり、一方で$k$が$|jc\alpha|$より十分小さい場合には、減衰系全体の変位に対して取り付けばねの変位が支配的になることが分かります。

すなわち取り付け剛性$k$を大きすぎない適切な値に設定している場合には、低速領域では粘弾性ダンパーの減衰係数が大きい（$k > |jc\alpha|$）ため、減衰系全体の変位に対して取り付けばねの変位が支配的になり、高速領域では粘弾性ダンパーの減衰係数が小さい（$k < |jc\alpha|$）ため、減衰系全体の変位に対してダッシュポッドの変位が支配的となります。
これは、減衰系の変位とダッシュポッド、取り付けばねの関係と対応しています。

2.2 取り付け剛性と解析安定性の関係

解析の安定性は不釣り合い力の大きさを目安にできます。ここでは、前ステップ(iステップ目)の計算による減衰系全体の増分変位を$\Delta X_i$とし、次ステップのダッシュポッド部分に作用する不釣り合い力$\Delta F_{c_{i+1}}$を考えます。

直列のため、$\Delta F_{c_{i+1}} = \Delta F_{i+1}$であることを利用すれば、

$$ \Delta F_{c_{i+1}} = K_{all} \cdot \Delta X_i $$

よって

$$ \Delta F_{c_{i+1}}　= \frac{k \cdot j c \alpha}{k+jc \alpha} \cdot \Delta X_i $$

従って

$$ \Delta F_{c_{i+1}}　= \frac{j c \alpha}{1+\frac{jc \alpha}{k}} \cdot \Delta X_i $$

本式より、不釣り合い力$\Delta F_{c_{i+1}}$は、$\frac{jc \alpha}{k}$について単調減少しますので、$k$が$|jc\alpha|$より十分大きい場合には、不釣り合い力が大きくなりやすく、一方で$k$が$|jc\alpha|$より十分小さい場合には、不釣り合い力が小さくなりやすい傾向にあると分かります。

すなわち取り付け剛性$k$を大きすぎない適切な値に設定している場合には、$k$が$|jc\alpha|$より大きくなりすぎることがなく不釣り合い力が小さくなり発散しにくくなります。

3. 並列な減衰装置の場合（内部剛性がダッシュポッドに対して並列に取り付くモデルの場合）

下図のような、ダッシュポッドと内部剛性が並列に存在する場合を考えます。
（ダッシュポッドに並列な内部剛性が複数存在する場合も同様です。）

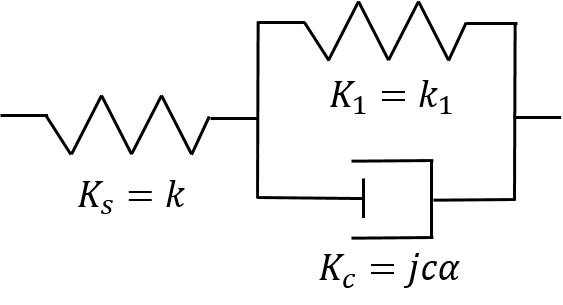
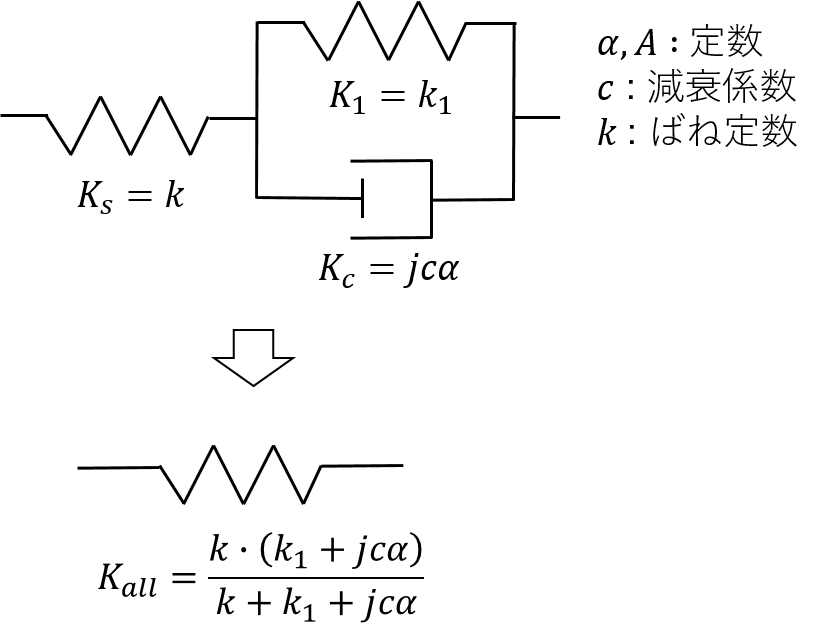
各々複素剛性を考えると、その合成された複素剛性$ K_{all} $は、

$$\large \frac{1}{K_{all}} = \frac{1}{K_s} + \frac{1}{K_c + K_1} $$

よって

$$\large K_{all} = \frac{k \cdot ( k_1 + j c \alpha)}{k + k_1 + jc \alpha} $$

と導けます。

3.1 取り付け剛性とダッシュポッド・取り付けばねの挙動の関係

外力$\Delta F$による、減衰系全体の変位を$\Delta X$とすると、

$$ \large \Delta X = \Bigl(\frac{1}{k} + \frac{1}{k_1 + jc\alpha}\Bigr) \cdot \ \Delta F $$

と導けます。$\frac{1}{k}$が取り付けばねによる変位、$\frac{1}{k_1 + jc\alpha}$がダッシュポッドの変位に対応しています。

直列の場合と入力される外力$\Delta F$が同じ場合、$k$が無限大となったとしても、並列に配置された内部剛性により外力による減衰系の増分変位$\Delta X$が直列の場合より小さくなります。これが後の収束性に関連してきます。

3.2 取り付け剛性と解析安定性の関係

前ステップ(iステップ目)の外力$\Delta F_i$による減衰系全体の増分変位を$\Delta X_i$とし、次ステップのダッシュポッド部分に作用する不釣り合い力$\Delta F_{c_{i+1}}$を考えます。

$$ \Delta F_{c_{i+1}}　= \frac{j c \alpha}{k_1 + j c \alpha} \cdot K_{all} \Delta X_i $$

よって
$$ \Delta F_{c_{i+1}}　= \frac{j c \alpha}{k_1 + j c \alpha} \cdot \frac{k \cdot ( k_1 + j c \alpha)}{k + k_1 + jc \alpha} \cdot \Delta X_i $$

従って
$$ \Delta F_{c_{i+1}}　= \frac{j c \alpha}{1 + \frac{k_1 + jc\alpha}{k}} \cdot \Delta X_i $$

本式より、一見すると直列の場合と同じく$k$が$|jc\alpha|$より十分大きい場合には、不釣り合い力が大きくなりやすく、発散しやすくなるように思えます。しかし、実際には取り付け剛性を無限大としても発散しないことがあります。これは、内部剛性$k_1$の効果により、前ステップ(iステップ目)の外力$\Delta F_i$による減衰系全体の増分変位$\Delta X_i$が、直列の場合と比較して小さくなるためです。（$\Delta X_i$について）

3.3 取り付け剛性が有限でありかつ非常に大きな値の場合

並列な減衰装置の場合、どんな取り付け剛性でも発散しにくくなるのでしょうか。
実は数値計算上の特性として、有限でありかつ非常に大きな剛性を与えると発散しやすくなります。
並列な減衰装置の合成複素剛性$K_{all}$は、

$$\large K_{all} = \frac{k \cdot ( k_1 + j c \alpha)}{k + k_1 + jc \alpha} $$
と表せました。

ここで、取り付け剛性$k$に⼤きな値を入力することを考えると、全体の複素剛性としては⼤きな値同士の割り算をすることになります。大きな値同士の割り算や掛け算を行うと、適切な計算ができない現象が発生することがあります。（情報落ちと呼ばれる現象です。）

実際の数値計算ではこのように減衰系を集約した形ではなく、剛性、減衰マトリックスを⽤いて⽴式し、その収束計算を実施しているため、この例は厳密ではありませんが、この例と同様に⼤きすぎる剛性を与えると、適切な計算が実⾏できない状態に陥ることがあります。

数値計算上の工夫として$K_{all}$の分母分子を$k$で除せば、$k$が大きい場合の情報落ちは防げます。一方で、$k$が0に近くなるような微小値の場合、分母で微小値による除算が生じるので発散しやすくなります。どちらを発散させにくくするかは、$k$に入力される値の想定次第になります。

まとめ

内部剛性が直列に配置されたモデルと並列に配置されたモデルに対して、複素剛性を考えることで取り付け剛性が無限大になった際の解析安定性を定量的に考察しました。
内部剛性による寄与の差によって取り付け剛性を無限大にした場合の挙動が異なることが分かりました。ただし、両者とも極端に大きな値を与えると発散しやすくなるため、弾塑性粘性ダンパーを用いる場合には

適切な大きさの取り付け剛性を与える
解析時間刻みを細かくする

などの工夫が必要になります。

求められた全体剛性からもわかる通り、取り付け剛性を無限大とした場合のモデルは、取り付け剛性が存在しないモデルと同値になります。RESP-Dの場合、取り付け剛性を空欄にしていただくことで取り付け剛性を無限大として入力することができます。

【構造解析Tips】粘弾性ダンパーの取り付け剛性と解析収束性の関係を複素剛性から考察する

粘弾性ダンパーの取り付け剛性と解析収束性の関係を複素剛性から考察する

目次

1. 複素剛性とは