RESP-Dで新たに対応したスパースマトリクスソルバについて解説します。以前からRESP-F3Tでは対応していましたが、RESP-Dでも利用可能となりました(メニュー項目「ツール」→「オプション」→「マトリクスソルバ」にて、Skyline(デフォルト)、Sparse、IntelPardisoの3種類から選択可能です)。
FEMやマトリクス法を勉強された方なら既にご承知のことかと思いますが、これらの計算理論では基本単位となるシンプルな要素の変形と応力の関係を記述して、節点(変位を未知数とする)を介して繋ぎ合わせて複雑な構造物をモデル化します。詳細な形状をモデル化しようとすると、細かく節点を配置してつなぎ合わせることになって、たくさんの節点を必要になります。たくさんの節点を介してつなぎ合わされていくということは、節点の数だけ未知数は増えてしまい、大きな未知数(多元)の連立方程式(剛性マトリクス)を解く必要が生じます。マトリクスソルバの議論は、この大きな多元連立方程式を如何に効率よく短時間で解くかという議論になります。
この議論のため、例として下図のような単純化(節点の未知数は1つ)した構造物を考えます。この構造物の連立方程式のイメージを下右図に示します(通常の構造モデルは、対角項を境とした対称行列になりますので上三角部分の係数のみを表示しています)。剛性マトリクスは、対戦表と同じで自由度同士の対戦の組み合わせが存在する箇所に剛性値が入っており、対戦が無い箇所はゼロとなります。例えば、10番の選手から見て対戦相手は3・9・11・17の選手になるので値が入りますが、その他は対戦が無いのでゼロ値となります。通常の対戦表では対角項は無意味ですが、剛性マトリクスの場合は大抵値が入る点が少し異なります。
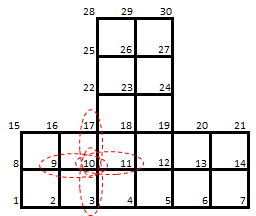

図1 構造物の自由度順と対応する剛性マトリクス
この対戦表を見て最初に気づくのが、試合数がスカスカだということです。連立方程式と聞くと、全ての項に値が入っているイメージがありますが、構造解析モデルの特徴として非ゼロ項は非常に少ない傾向があり、このような状態を疎行列(英語ではSparse Matrix)と名づけています。構造モデルが大きくなればなるほど、非ゼロ項の比率は小さくなる(疎の傾向が強まっていく)傾向があります。
構造計算においては、この剛性マトリクス([K])に対して外力項({F})が作用した場合の変位({X})を求めますので[K]×{X}={F}と方程式が立ち、連立方程式の解を求める計算を行うことなります。連立方程式の求解にはガウスの消去法に類する演算が行われますが、上図のマトリクスを解く過程において下図のように非ゼロ項が大量に出現して、疎な状態が密に近づくことが問題となっています。

図2 消去演算中に発生するフィルインの状況(×マーク:フィルイン箇所)
図中の×マークは、演算中に非ゼロが発生する箇所(フィルインと呼ぶ)を意味します。ここで2点の特徴に気づかれると思います。1点目は、構造モデルの端から連番で自由度番号を付けると非ゼロ項は対角項に近い場所に分布する傾向があること。2番目は、せっかくの疎行列でも消去演算を行うとフィルインによって非ゼロ項が大幅に増えてしまうということです。実際の計算量としては、最初から値が入っている箇所(グレーのセル)だけでなくフィルインの箇所(×マーク)も含めて計算対象なりますので、それ以外の空欄を最初から無視できれば、省メモリ+計算量削減の一石二鳥となり、効率の良いプログラムになります。
最初に考え出された方法が、バンドマトリクス法です。下図のように右上三角形の部分を最初から無視して、対角項に対して帯状の領域(バンド領域)のみ考慮できれば、プログラムのシンプルさを失わない中で大幅に必要メモリ量を低減し、同時に計算量を減らすことができます。フィルイン(×マーク)だけでなく、バンド内に多くのゼロ項(グレーの空欄)も含んでしまっていますが、フルマトリクスに比べれば劇的に必要メモリ量・計算量を減らすことができます。
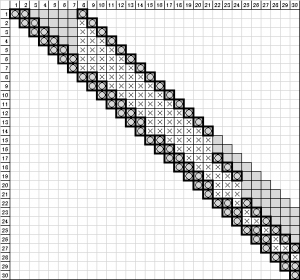
図3 バンドマトリクス法による値の保持方法
次に考え出された方法が、番号付けによる最適化(リオーダリング)です。下左図のように番号を付け替えると、下右図のようにバンド幅を縮小することができます。具体的には、上図がバンド幅8(計算領域としては、8×30-7×8÷2=212)だったものが下図ではバンド幅6(計算領域としては、6×30-5×6÷2=165)に減少できています。ただし、ベストな最適化を目指そうとすると本来の方程式の求解自体よりも時間がかかってしまいますので、経験的手法によるベターを目指すことが現実的となります。
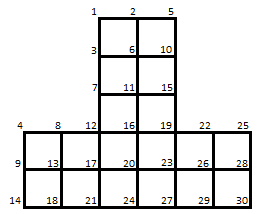

図4 バンド幅縮小の最適化の効果
上図をよく見ると、バンド領域の中にも最初から最後までゼロのままの空欄が残されていることが分かります。ここを削除することができれば、さらに効率を向上させられると考えられます。それを実現したのがスカイライン法です。この方法では、自由度毎に高さの情報を持つため、稜線が高層ビルの夜景のようになることから名付けられています。上図では、このような空欄は25個ありますが、下図のようにスカイライン法ではフィルインも含めた非ゼロの場所のみ保持しますので、計算領域としては最適化したバンドマトリクスの165から140まで減らすことができます。
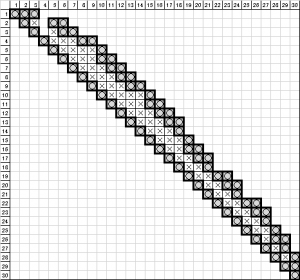
図5 スカイライン法による値の保持方法
上図を眺める限り、最適化としては限界かなと思う訳ですが、実務の構造モデルになると普通に数万自由度となりますので、プログラムが多少複雑になろうともさらに強力な最適化を進めたいという要求が出てきます。そのような要求から、次に考えられたのは連続領域に捕らわれず、疎行列のまま保持すること(スパースマトリクス法)を前提とした最適化法です。いくつか方法が提案されていますが、代表的な方法としてMD(Minimum Degree:最⼩次数序列)法を示します。バンドマトリクス法やスカイライン法のように対角項に寄せるという方向性を捨てて、徹底的にフィルインが少なくなるように順序付けしていく方法です。方程式の求解プログラム(マトリクスソルバ)は飛躍的に複雑になりますが、その効果は大きく下図のように番号付けを行うと、スカイライン法のフィルイン数が63だったのがMD法では38まで減らすことができます。
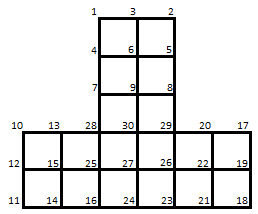
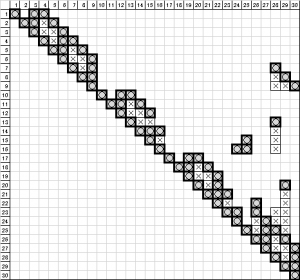
図6 MD法による最適化の効果
各最適化手法の効果をまとめると下表にようになります(表中の演算量の比は、単純に必要メモリの比の3乗で算出しています)。実務での立体構造解析では、一般的に数千~数万の自由度数になりますので、これら手法による差はさらに広がることになります。
表1 各手法による最適化の効果の比
| 方法 | 計算対象数 | 必要メモリの比 | 演算量の比 |
| 三角マトリクス | 465 | 2.19 | 10.55 |
| バンドマトリクス法(非最適化) | 212 | 1.00 | 1.00 |
| バンドマトリクス法(最適化) | 165 | 0.78 | 0.47 |
| スカイライン法 | 140 | 0.66 | 0.29 |
| スパース法(MD法) | 115 | 0.54 | 0.16 |
実際のマトリクスソルバのプログラミングにおいては、プログラム自体の複雑さや演算装置の構造による影響(キャッシュメモリのヒット率やスーパースカラーや複数CPUコアによる並列処理)も絡んできますので、単純に非ゼロ項を減らすことが必ずしも時間短縮につながらないことがあり、RESPのようなビル構造物の解析ではデフォルトのマトリクスソルバとしてスカイライン法を採用しています。しかし、層の飛び越し部材が多いビル建物や大空間構造物では疎性を活かした方法の効果が絶大で、数十倍の計算時間の差が出ることは珍しくありません。
RESP-Dで新たに選択可能となったSparse(今回紹介したMD法を含む複数の方法によって番号付けを最適化し消去演算を並列に行う手法)や、IntelPardiso(米国Intel社が自社CPU向けに最適化したPARDISO(スイスのバーゼル⼤学で開発されている疎行列ソルバの高性能ライブラリ)の背景にある技術を理解して、使いこなしていただければと思います。