固有周期とオイルダンパーの関係
一般的な固有値解析では減衰項は考慮されないため、減衰によって固有周期がどう変わるかはあまり意識されないことが多いと思います。
実際、建物全体の減衰定数(内部粘性減衰)による固有周期の変化はごくわずかであることがほとんどかと思います。
減衰が大きくなるとブレーキのような働きとなるため、固有周期はわずかですが長くなる方に変化します。
一方で、オイルダンパーのような支持剛性を持つダンパー要素の場合、直列剛性が作用することにより固有周期が短くなることがあります。
これは複素固有値解析をすればわかってくるのですが、直感的に理解しにくい現象でもあるため、1質点系モデルで検証してみました。
検証
ダッシュポットを増やした場合
まず、1質点に対して単純なダッシュポットを付与した場合の応答解析を行います。
入力波は正弦波とし、1質点の1次固有周期1秒に合わせ、1秒だけ入力したあとは自由振動させています。
減衰の大きさを5段階に変化させています。
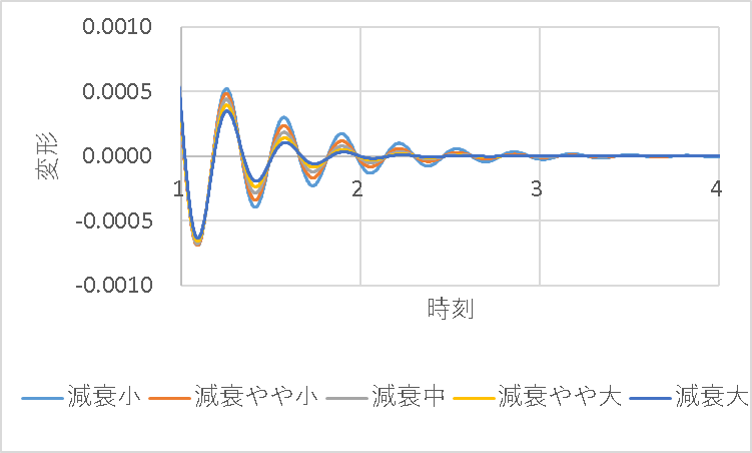
結果の通り、当然減衰を大きくするほど振幅は小さくなります。
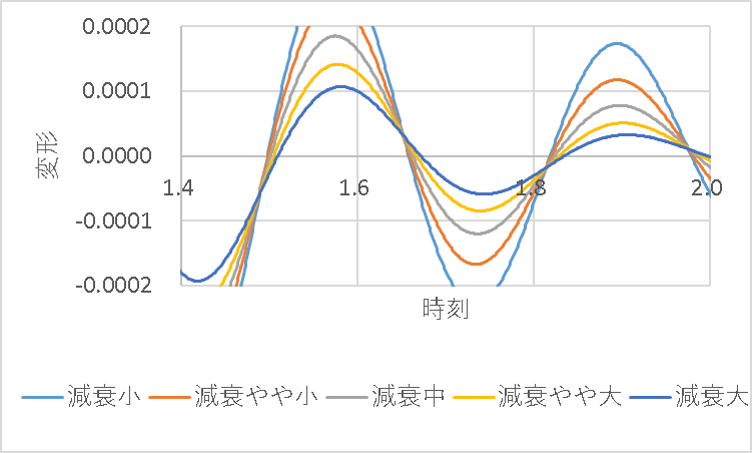
また、以下に一部の時刻について拡大した図を示します。
変形0のX軸位置を横切る時刻に着目すると、減衰を増やすとわずかばかりですが、周期が長くなる方向に変化していることが確認できます。
これが、ブレーキのような効果で周期がわずかに長周期化しているような現象となります。
オイルダンパーを配置した場合
続いてオイルダンパーを配置した場合です。
支持剛性は、減衰に比例して増大させています。
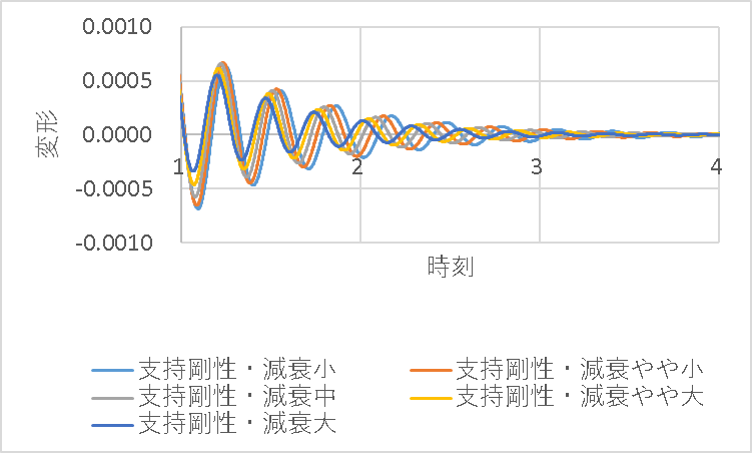
減衰を大きくすると振幅が小さくなるのは同様ですが、減衰が大きくなるほど今度は逆に周期が短くなってきているのが見て取れます。
前述のように、支持剛性が完全に剛となるダッシュポットでは周期がむしろ長くなる方向なので連続しない関係性となりますが、有限な支持剛性を有していると減衰力が発揮されたときにダンパー支持剛性が架構の剛性に加算されるような形で作用してしまうために、このような現象が生じます。
ダンパー量が多い場合には、今回のように無視できないほど周期が変化する場合があります。
学んだこと
実はこの検証は、ある物件において建物固有周期と地震波のスペクトルを見比べて最大応答になるであろう地震波を予想していたのですが、予想に反してより短周期で大きな応答成分を持つ地震波がクリティカルになったことが発端となりました。
教訓として、速度依存ダンパーによる制振の場合は短周期化も視野にいれて最大応答地震波を選定する必要があるケースがあるということを学びました。
皆さんの参考にもなりますと幸いです。