モード特性について
低次元化には元のモデルの固有値解析結果を使います。 非減衰系の一般化固有値問題を解いた固有ベクトルは質量マトリクス、剛性マトリクスを対角化する事が出来ます。この対角成分をモード剛性、モード質量といいました。$$
Φ^\top M Φ = \left(
\begin{array}{cccc}
M_{ 1 } & 0 & \ldots & 0 \\\
0 & M_{ 2 } & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & M_{ n }
\end{array}
\right)
$$
$$
Φ^\top K Φ = \left(
\begin{array}{cccc}
K_{ 1 } & 0 & \ldots & 0 \\\
0 & K_{ 2 } & \ldots & 0 \\\
\vdots & \vdots & \ddots & \vdots \\\
0 & 0 & \ldots & K_{ n }
\end{array}
\right)
$$
任意の自由度を1.0として基準化する
固有ベクトルの任意の自由度を1.0にして基準化すると、その自由度で振動する時の等価質量となるモード質量が得られ、物理的な意味がはっきりします。 例えば、(1)の固有モードが速度 vで振動する時の各自由度の速度は(2)のようになります。$$ \lbrace x_1, x_2 , \cdots ,x_n \rbrace ^T \tag{1}$$
$$ vx_1, vx_2 , \cdots , vx_n \tag{2}$$
(m_n)をn番目の節点の質量とすると系全体の運動エネルギーは次のようになります。$$ \frac{1}{2}\ ( m_1 v^2 x_1^2+ m_2 v^2 x_2^2 + \cdots + m_nv^2x_n^2 ) \tag{3}$$
この中でj点に注目し、 j点の等価質量を (M_j)とすると等価1自由度系としてのエネルギーは次の様に表せます。$$ \frac{1}{2}\ M_j v^2x_j^2 \tag{4}$$
このモードの全体のエネルギーを着目した点で集約していると考え、(3)、(4)が同じエネルギーとすると次のようになります。$$ \frac{1}{2}\ M_j v^2x_j^2 = \frac{1}{2}\ ( m_1 v^2 x_1^2+ m_2 v^2 x_2^2 + \cdots + m_nv^2x_n^2 ) $$
$$ M_j = m_1 \left( \frac{x_1}{x_j}\right)^2+ m_2 \left( \frac{x_2}{x_j}\right)^2 + \cdots m_2 \left( \frac{x_j}{x_j}\right)^2 \cdots + m_n\left( \frac{x_n}{x_j}\right)^2 $$
これをマトリクス表示する次のようになります。$$
M_j =
\begin{pmatrix} \frac{x_1}{x_j} \\\ \frac{x_2}{x_j} \\\ \vdots \\\ \color{red}{\frac{x_j}{x_j}} \\\ \vdots \\\ \frac{x_n}{x_j} \end{pmatrix}^T
\left(
\begin{array}{cccccc}
m_{ 1 } & 0 & \ldots & \ldots & \ldots & 0 \\\
0 & m_{ 2 } & \ldots & \ldots & \ldots & 0 \\\
\vdots & \vdots & \ddots & \ldots & \ldots & 0 \\\
\vdots & \vdots & \vdots & m_{ j } & \ldots & 0 \\\
\vdots & \vdots & \vdots & \vdots & \ddots & 0 \\\
0 & 0 & 0 & 0 & 0 & m_{ n } \
\end{array}
\right)
\begin{pmatrix} \frac{x_1}{x_j} \\\ \frac{x_2}{x_j} \\\ \vdots \\\ \color{red}{\frac{x_j}{x_j}} \\\ \vdots \\\ \frac{x_n}{x_j} \end{pmatrix}
$$
低次元化方法
まず低次元化をする自由度を決めます。その自由度での等価質量を求めて、その平方根で除して基準化します。$$ \frac{Φ_i}{ \sqrt{ M_ij } } $$
(Φ_i)はi次の固有ベクトル、(M_ij)はi次のj番目の自由度の等価質量です。これは質量マトリクスを固有ベクトルの掛け算に分解した形となります。固有振動数を使えば、剛性マトリクスも表現する事ができます。
$$
M =(ΦΦ^\top)^{-1} \tag{5}
$$
$$
K = {Φ^\top}^{-1} Ω^2 {Φ}^{-1} \tag{6}
$$
$$
\begin{pmatrix} \ \color{red}{-1.09}\\\ -0.40 \\\ 0.52 \\\ \color{red}{1.0} \\\ 0.77 \end{pmatrix}
$$
→
$$
\begin{pmatrix} \ \color{red}{-1.09} \\\ \color{red}{1.0}\end{pmatrix}
$$
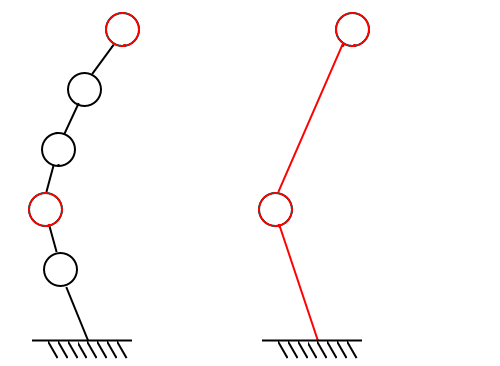
しかし、出来上がった質量マトリクスは任意の値を抽出した固有ベクトルを使うので質量連成項が現れます。例えば前回の例題で計算してみると次のようになりました。 質量連成がなくなるように固有ベクトルを修正します。この修正は連成項が0になるような固有ベクトルで有れば良いのですが、なるべく元の固有ベクトルと近くなるよう修正量がノルム最小解となるような修正をします。 こうして修正された固有ベクトルから作られた質量マトリクスは集中形となり、低次元化がされました。修正後の固有ベクトルを(6)にも適用すれば低次元化された剛性マトリクスも作成できます。

閑話 ー 前回のクイズの答え
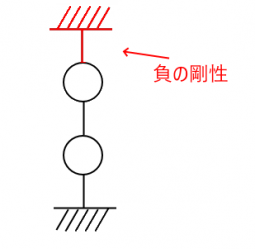
前回、この剛性マトリクスには工夫があるという事でしたが、分かりましたでしょうか。答えは一番上の質点に負の剛性を持ったバネを使っている事です。 串団子の質点系モデルで全体剛性マトリクスを作成すると三重対角行列となります。一番上の質点はバネが一つ付いているだけなので、連成項と最上の対角成分の値は符号を入れ替えただけとなります。例えば4質点系の串団子モデルで剛性マトリクスを作成すると以下のような形になります。$$
\left(
\begin{array}{cccc}
K_{ 1 }+ K_{ 2 } & - K_{ 2 } & 0 & 0 \\\
- K_{ 2 } & K_{ 2 }+ K_{ 3 } & - K_{ 3 } & 0 \\\
0 & - K_{ 3 } & K_{ 3 }+ K_{ 4 }& \color{red}{-K_{ 4}} \\\
0 & 0 & \color{red}{- K_{ 4 }} & \color{red}{K_{ 4}}
\end{array}
\right)
$$
$$
\left(
\begin{array}{cccc}
1.43×10^{8} & -6.85×10^{7} \\\
-6.85×10^{7}& 6.85×10^{7} \color{red}{-1.11×10^{7}}
\end{array}
\right)
$$