【RESPチーム四方山話】任意形状の床の荷重計算について

まず初めに、RESPではこの記事の方針で荷重計算をしておりません。あくまで私が考えたやり方という記事ですのでその想定でお読みになっていただければと思います。
RESP-Dの荷重計算処理については別の記事でご紹介いたします。

荷重計算について

構造計算プログラムで床荷重は単位面積当たりの重量として入力していますが、内部計算において長期荷重を考える時にその重量を周辺の大梁もしくは小梁への分布荷重として考えます。多くのプログラムではこの計算を「準備計算」と称して「架構認識」が終了した後に行っています。
この時の分布荷重の形状は床領域の各頂点から二等分線を引いて交点を結ぶことでできる形状となります。いわゆる亀の甲分割です。凸多角形の四角形であるなら各二等分線同士がぶつかるのでその交点同士を結んで床割が終了です。 しかし、五角形以上となると、「二等分線の交点で結ぶ」というルールだけではほとんどの場合で交点がない二等分線があるので、もう少し複雑なルールに拡張する必要があります。
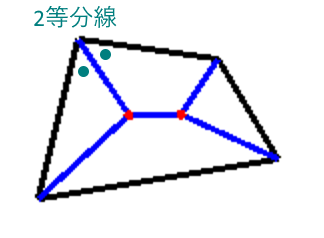
以前、私なりに考えたやり方を記載してみます。

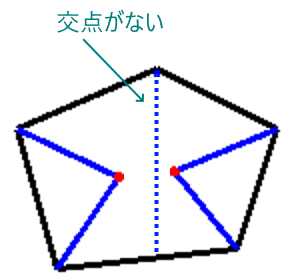
図形を〇〇の集合として考えてみる

突然ですが、「円」の定義をご存じでしょうか。絵はすぐに浮かびますが、正式な言葉として表現すると、意外に答えあぐねる事はないでしょうか。
答えは「ある定点から距離の等しい点のすべての集合」です。このように図形を「〇〇の集合」として考えてみるといつもと違った印象になり本質が見えてくることがあるので、よくこのように考えています。

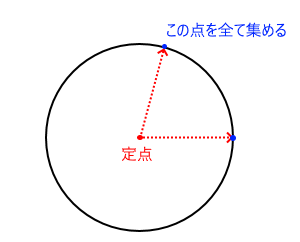
亀の甲分割はどんな集合を作っているか

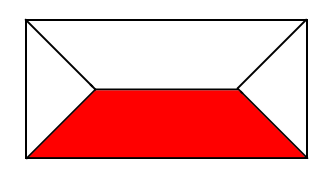
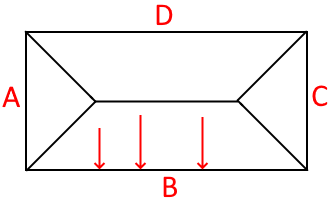
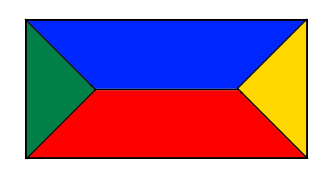
では、荷重計算時に使われる亀の甲分割による床割はどんな集合を作っているのかを考えてみます。前述の通り、亀の甲分割は各頂点から二等分線を引いてぶつかりあう点で区切って分布荷重を作成します。簡単な長方形で考えてみます。 赤い領域が南側の辺が負担する分布荷重です。じっと見てみると「作成された分布荷重は微小領域で一番近い辺が同じだな」と直感的にわかると思います。言い換えると「南側の辺が一番近くなる点のすべての集合」といえると思います。※境界部分などの細かいことはまだ考えません。
下図で赤い面の領域はどの箇所を選んでも一番近い辺がBとなります。

これは、床とその周辺を支持する大梁があった時に、亀の甲分割で荷重を作成すると、「床の微小領域の重量は一番近い大梁が負担する」ということなので、物理的な直感とも一致します。

亀の甲分割を区切る線はどんな集合

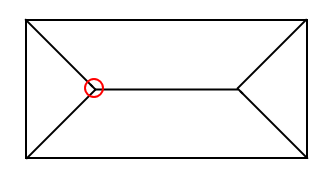
次に分布荷重を区切っている線はどんな集合と呼べるかを考えてみます（下図の赤い線）。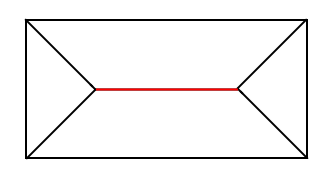
この区切っている線は下の赤い集合と青い集合の境界で両方に属しています。二つの集合の属性を兼ねており、「辺Bが最近辺となる」と「辺Dが最近辺となる」を両方持っています。 この線上はどの点をとっても辺Bと辺Dが最も近い辺になります。
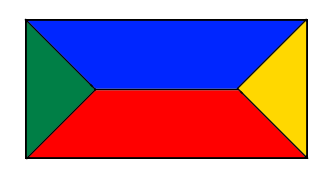
他の同様の区切っている線を確認しても、いずれかの2つの辺に最短距離を持つ点の集合になっています。
したがって、分布荷重を区切る線は「最短距離となる2つの辺が等しい点のすべての集合」となっています。

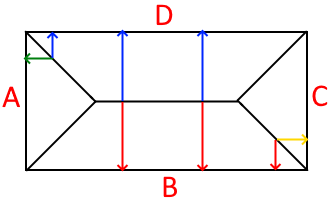
区切る線を結ぶ点はどんな集合

最後に区切る線を結んでいる点はどんな集合かを考えます。今までの流れで同様に考えると、「最短距離となる3つの辺が等しい点のすべての集合」 となります。点なので集合と言っていいのかと思う方もいるかもしれませんが、「単集合」というれっきとした集合です。この点と頂点を結べば分布荷重が出来そうです。 ただ、この反証の一つはすぐにわかると思います。例えば、正方形の床の場合は荷重分布は二等辺三角形となり、 「区切る線を結ぶ点」は4つ全ての辺に対して最短距離が等しい点となります。最短距離となる辺の数が3の場合、4の場合が出てきました。

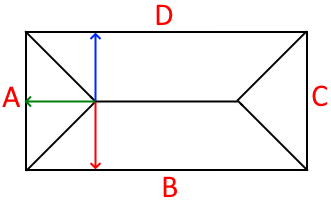
最終的に何個の辺に対して最短距離が等しければいいのか

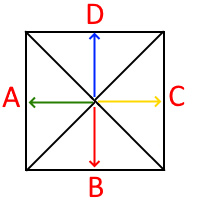
現在、考えているのは面が集まって点になる箇所です。その面は「1つの辺に対して最短距離が等しくなる集合」という図形で、この面が集まった点は、「各面が最短距離とする辺」のすべてを最短距離の辺となる点です。
面をいくつ必要とするかを考えるために多面体を想像してみます。多面体の頂点は「面が集まって点になる箇所」です。多面体の頂点は少なくとも３つの面が集まる必要があるので、展開図を想像して同じように考えてみます。
つまり、「少なくとも3つ以上の辺に最短距離が等しい点」を探して結べばどんな図形であっても、「床の微小領域の重量は一番近い大梁が負担する」 ような分布荷重を作成できそうです。

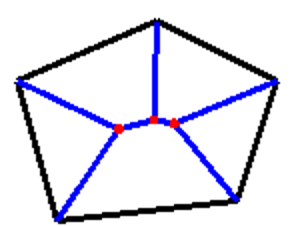
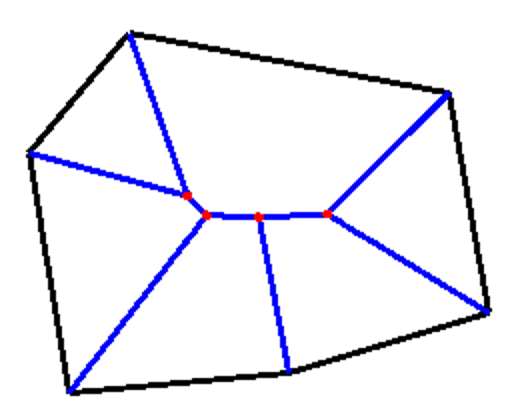
実際に五角形以上に適用してみる

この「少なくとも3つ以上の辺に最短距離が等しい点」というルールで任意の凸多角形に適応してみると次のような絵になります。座標がわかっているので、普通の亀の甲分割した時と同じ要領で分布荷重を考えることができます。描いてみると「二等分線の交点だけで求まらない点」は「二等分線同士の二等分線の交点」となっていそうで、既存の考え方を拡張すればプログラムを作成できそうです。
ただ、アルゴリズムとしては「少なくとも3つ以上の辺に最短距離が等しい点」という一つのルールに沿って考えた方がシンプルな気がするので考え方によってはこちらの方が組みやすいと思います。

問題点（凹多角形の場合）

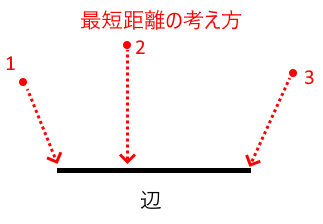
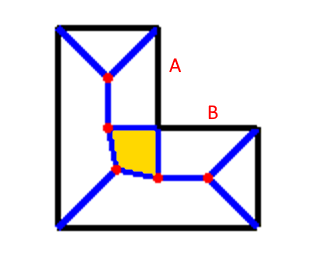
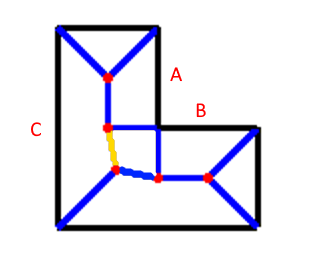
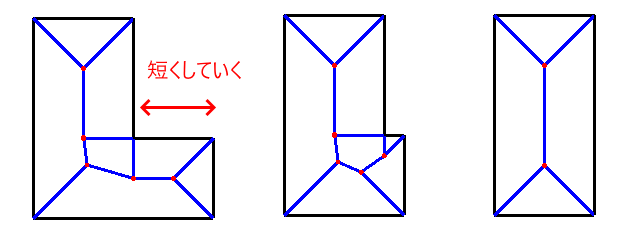
ここまでの説明でことあることに「凸多角形」を強調してきましたが、「少なくとも3つ以上の辺に最短距離が等しい点」というルールだけでは「凹多角形」に対応できません。1例としてL字の床を想定します。 「点と線の最短距離」は点から線に向かった垂線（上左図の2）ですが、今回は「荷重を負担するのに最も近い場所」という考えが元になっているので、辺の両端の垂線の範囲から外れている場合は両端までの距離を最短距離と考えます(上左図の1と3）。その場合は上右図の黄色い領域は辺A、Bにが最近辺となり今までとは考えが異なる領域が出てきます。この場合は黄色い領域は辺A、Bの交点に節点荷重として渡すのが直感的です。 次に、下図で黄色い部分は辺A、B、Cを最近辺とするはずですが、実質A、Bの交点と辺Cの最短距離となるので、「少なくとも3つ以上の辺に最短距離が等しい点」というルール上はこの部分は直線ではなく曲線となるはずです。この部分が曲線分布荷重とできれば「床の微小領域の重量は一番近い大梁が負担する」という事を完璧に実現できると思います。 このような事を考えると、いろいろ制約が追加されていき最終的には割と複雑なソースになってしまいました。作成当時は完成させるために「少なくとも3つ以上の辺に最短距離が等しい点」をベースにしていきましたが、もう少しすっきりしたルールが作れないかは今でもたまに考えることがあるので、何か良い案が出たらまた記事にしたいと思います。
ただ、出来上がったプログラムでいろいろ検証してみるとL字の腕の部分を徐々に短くしていくと、普通の長方形の亀の甲の形に近づいていく様子がわかるのでこの点は面白いなと思います、

まとめ

今回は五角形以上の多角形の床割について、「集合」を使って考えてみました。プログラムを組む時のルールはなるべくシンプルな方が良いので、その意味では二等分線を繰り返してつないでいくことよりは複雑な実装にはならないと思っています。その分、ソースコードを見て直感的な理解は難しいかもしれませんが、考え方がわかる資料さえあれば問題はないと思います。
気づいた方もいたかもしれませんが、厳密に幾何学的な証明にはなっていません。一応、実用上問題はないので「私は消化のプロセスを知らないからといって、目の前のごちそうを我慢することはない」と思っています。
先にも書きましたが、改良の余地はあると思うので、この記事を読んでもう少し良いアプローチや表現があればコメントでお寄せいただけますと幸いです。