【RESPチーム四方山話】複素固有値解析一考～解析の定義と結果の変わり方～

複素固有値解析について

RESP-DやRESP-F3Tには「複素固有値解析」の機能が付いています。普通の固有値解析との違いは減衰を考慮できるという点ですが、慣れてないと解析を実行してみても解釈が難しい場合があります。「複素固有値解析」がどんなものかを何回かに分けて記載することで、ハードルを下げるきっかけになってもらえればと思います。
RESPブログでは以前にも「複素固有値解析」を取り上げてましたが、今回は数値解析が強めの記事となります。後半になるにつれ趣味全開になるかもしれませんが、温かく見ていただけると幸いです。

定義について

質量マトリクスM、減衰マトリクスC、剛性マトリクスKとなる振動系があった時に、複素固有値解析は次の行列Aの固有値問題のことを指しています。 式の導出についてはRESP-F3Tマニュアルの計算理論編もありますので、そちらを参照してください。※インターネットで検索してもいろいろ記載があります。
このA行列の中に減衰マトリクスを含んでいるため、減衰が考慮できるというものになっています。この行列の固有値は一般的に複素数となり、これが複素固有値解析と呼ばれる所以です。見てわかる通り、A行列は「非対称行列」です。工学に出てくる固有値問題の多くは「対称行列」に対するもので、インターネットで検索すると出てくるアルゴリズムは多くが「対称行列」にしか適用できないものです。昔の名言で「対称行列の固有値問題はサイエンスだが、非対称行列の固有値問題はアートである」というものもありました。

「普通の固有値解析」は剛性マトリクスKと質量マトリクスMを使うので「MK型固有値解析」、複素固有値解析は減衰マトリクスＣを含むので「MＣK型固有値解析」と呼ばれることもあります。

固有周期、減衰定数はどのように決まるのか

普通の固有値解析は質量分布と剛性分布で結果が決まります。複素固有値解析は当たり前ですが、質量、剛性、減衰のバランスで周期、減衰定数が変わります。振動解析の時は剛性比例減衰を与えることが多いですが、純粋な比例減衰の場合は固有周期、減衰定数はわかりやすい結果となります。
4パターンの解析事例でイメージを膨らませてみましょう。
①：ダンパーなしで1次の周期に対して2％の減衰を与える（比例減衰となる）
②：ダンパーなしで2次の周期に対して3％の減衰を与える（比例減衰となる）
③：オイルダンパーを含む（非比例減衰となる）
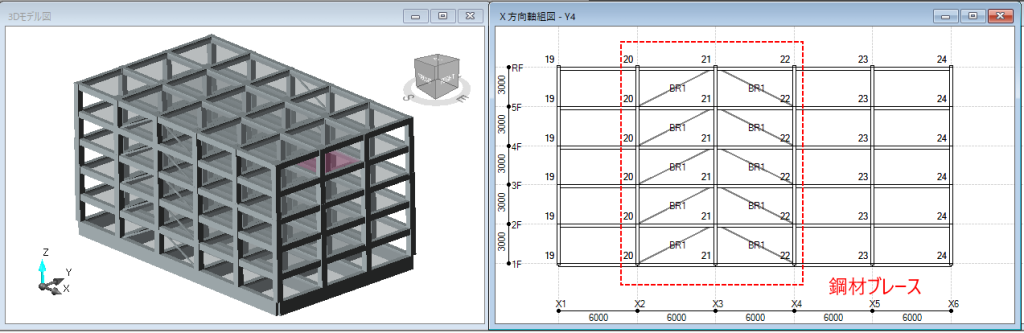
④：鋼材ダンパーを含む（非比例減衰となる）
①、②は減衰定数が変わらない例で、③、④は減衰定数が変わる例となります。

①：1次の固有周期T1に対して減衰定数2％として減衰マトリクスを作成した場合、複素固有値解析結果は1次の固有周期がT1、減衰定数が2%となります。 ②：2次の固有周期T2に対して減衰定数3％を与えた場合は、複素固有値解析結果の2次が固有周期がT2、減衰定数が3%となります。 剛性が変わらずに、剛性分布と減衰分布のバランスも変わらないので、普通の固有値解析と複素固有値解析で固有周期が変わりません。
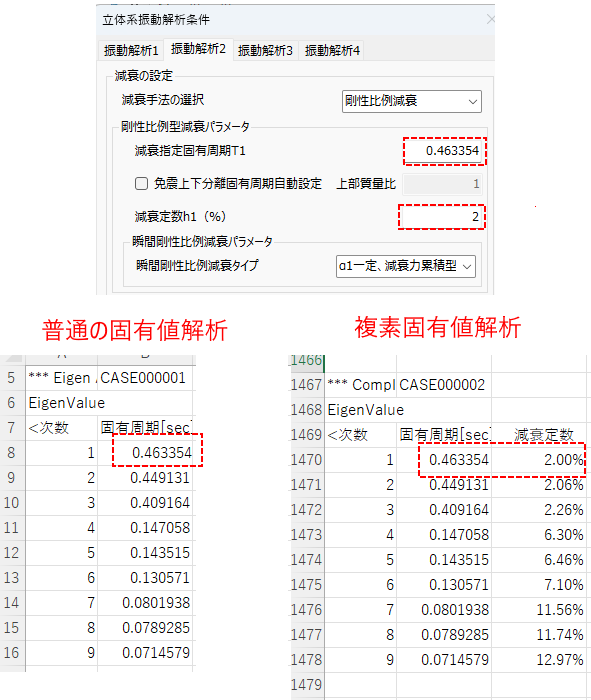
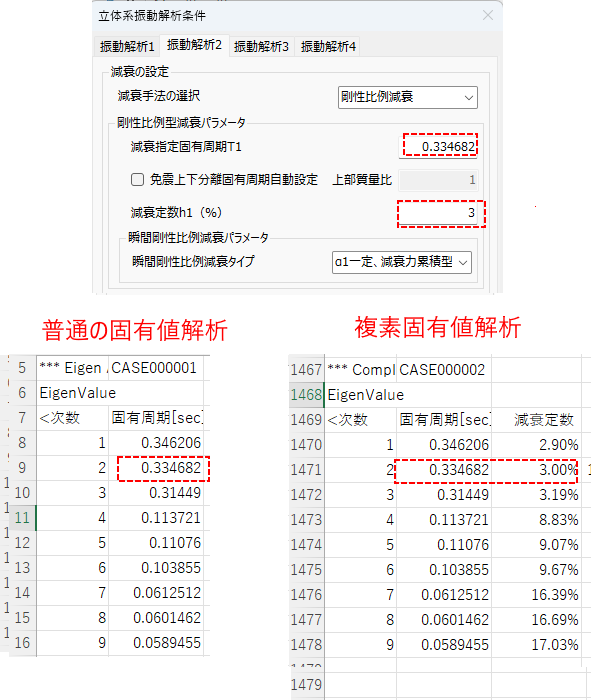
単純な比例減衰だと単純にわかりやすいですが、ダンパーなど剛性に比例しない減衰をモデル化すると、このバランスが崩れるので減衰定数、固有周期が変わります。
③：①のデータに単純なダッシュポットでモデル化するダンパーを入れた場合は減衰定数が増えて、固有周期が短くなっています。単純なダッシュポットとして配置しているため、通常の固有値解析結果は変わりません。通常、減衰が大きくなると建物は長周期化する傾向にありますが、ロッキングに効くようなダンパー配置の場合は見かけの剛性が大きくなり、固有周期が短くなることもあります。

④：②のデータに座屈拘束ブレースを配置してみます。剛性が高くなるので普通の固有値解析結果でも固有周期は短くなります。RESP-Dでは履歴系ダンパーの内部粘性減衰定数を0としてモデル化します。②のデータは2次の周期に対して3％の減衰を与えていましたが、剛性だけに考慮されて、減衰マトリクスに影響しないので、減衰定数が3％よりも小さくなります。

ダンパーの種類によって、どのような結果になるかのイメージはつきましたでしょうか。
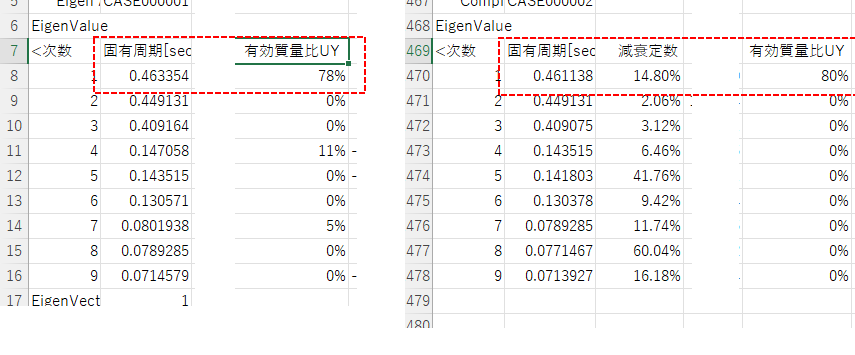
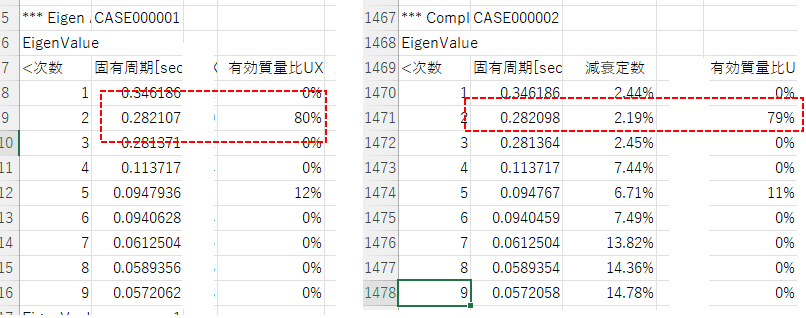
ちなみに、④が座屈拘束ブレースではなく通常の鉄骨ブレースであれば、減衰マトリクスに加味されるので①と②と同じ傾向で固有周期が変わらず、指定した次数に設定した減衰定数が複素固有値解析結果として出てきます。

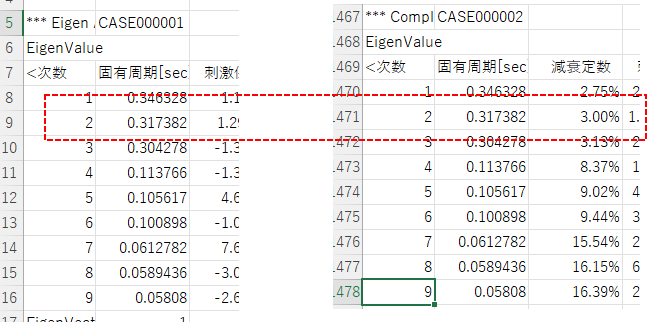
減衰定数の増減について

①～④の検証を総じて、ダンパーの影響を見たい場合は、元々の減衰マトリクスにおいて、何次の周期に対して何％の減衰定数を考慮したかを意識してください。
例えば、全体2次の周期に対して、3%の減衰を与えた場合に、複素固有値結果の全体1次の減衰定数が3％と比べてどうなっているかを見ても、ダンパーの影響を知ることができません。
そして、履歴ダンパーを使うと複素固有値解析は元々与えた減衰定数より小さくなります。履歴ダンパーは履歴減衰を付与する発想のため、減衰マトリクスに影響せず複素固有値解析ではその減衰効果を評価できません。オイルダンパーと併用した時に減衰定数の増減に注意してください。
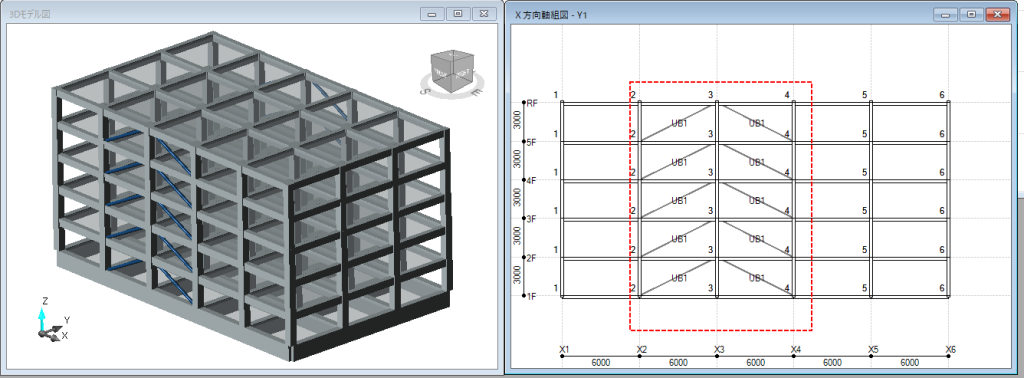
ダンパーをX方向に配置しているのか、Y方向に配置しているのか、ダンパーが剛性・減衰マトリクスにどのように影響するのかを考えながら分析するとより理解が深まると思います。

閑話：複素固有値解析という呼び方について

よく考えると、「複素固有値解析」という呼び方は不思議ではあります。行列に何も制約を入れなければ固有値はほとんどの場合「複素数」だからです。通常の固有値解析は扱う行列が実数のみの対称行列であるから、固有値が「実数」となっているだけで、むしろ、普段やっている固有値解析の方が特殊な場合と捉えた方が自然な気がしています。そういう意味では、「複素固有値解析」は「減衰を考慮した固有値解析」や前述の通り「MＣK型固有値解析」と呼ぶのが直接的な印象です。

まとめ

今回は複素固有値解析の導入として、どういう計算しているか、ダンパーの影響でどのように結果が変わるかを掲載してみました。
次回は複素固有値解析の解法に関する記載をします。