等価曲げせん断型質点系振動モデル
等価曲げせん断型とは
以前の記事では、最も基本的な質点系振動モデルである等価せん断型について説明しました。簡単そうで奥が深い質点系振動モデルの話 その1
今回の記事では、もう少し詳細なモデルとして等価曲げせん断型について説明します。
なお、今回紹介するモデルは、文献によって異なる呼称が用いられています(等価曲げせん断型または曲げせん断棒モデル)。本記事では、以下の文献の1) にならい、「等価曲げせん断型」として記載します。
<参考文献>
1) 「評定・評価を踏まえた高層建築物の構造設計実務」財団法人 日本建築センター (p.86 に「等価曲げせん断型」の記載)
2) 「建築構造物の動的性状と解析 学びやすい構造設計」日本建築学会 関東支部(p.56に「曲げせん断棒モデル」の記載)
等価せん断との違いは?
まず、等価曲げせん断型と等価せん断型との違いについて説明します。 等価せん断型が各階の変形をすべてせん断変形だととらえているのに対し、等価曲げせん断は各階の変形がせん断変形と曲げ変形で構成されているという考えでとらえるという点が異なります。つまり、各層の変形がほとんどすべてせん断変形だととらえて差し支えない場合には、等価せん断モデルで十分、そうでなければ等価曲げせん断とするほうが精度が高まる、ということになります。具体的には、低層の建物や塔状比が小さい建物であれば、等価せん断で十分ということになります。曲げ変形の正体
曲げ変形を理解するために、まず各階の変形がどのような成分で構成されるかを整理します。せん断変形が層せん断力によって発生する各層が水平移動することによる変形であるのに対し、曲げ変形は柱の軸伸縮によって生じる各層の回転(傾き)から生じる変形です。ここで、各階の全層間変形をδ、せん断変形をδs、曲げ変形をδmとおくと以下のようになります。
$$\large \delta = \delta_s + \delta_m $$
このδmが曲げ変形と呼ばれるものです。図で表すと、各変形は以下のような概念になります。
 せん断変形 曲げ変形
せん断変形 曲げ変形
なぜ等価曲げせん断型が必要か
先程の各変形成分に対し、層せん断力をQ, 層剛性をKとおいた場合、以下のように層の水平変形δ(せん断変形+曲げ変形)により層せん断力と層剛性の関係を算出するのが等価せん断型です。$$\large Q=K・δ=K・( \delta_s + \delta_m ) $$
一方、等価曲げせん断型の層剛性Kは以下のように、せん断変形のみで層せん断力と層剛性の関係を定義します。 $$\large Q=K・\delta_s $$
ここで重要なことは、せん断変形δsは同じせん断力が発生した場合には外力分布形によらずに同じ値となりますが、曲げ変形δmはモーメントによって変化するということです。そのため、等価せん断型では同じせん断力が発生している階でも、外力分布形が異なり転倒モーメントが異なれば層剛性が異なります。
この曲げ変形の影響は、設計用の外力分布形が多少変わった程度ではそれほど差は生じません。この影響が問題になるのは、1次以降の高次モードによる外力分布が作用したときです。
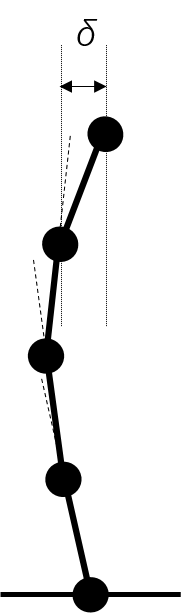
以下に、1次モードと2次モードが生じた場合の質点系振動性状のイメージ図を示します。
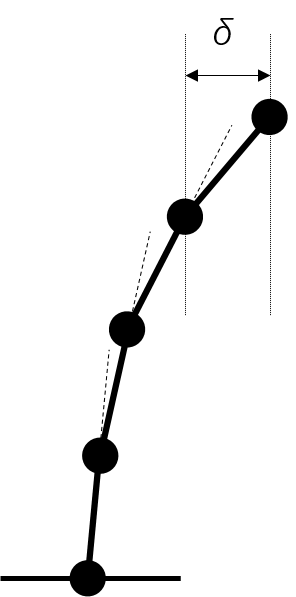
左 : 1次モード
右 : 2次モード
等価せん断型のモデルとする場合は、層間変位δからばね値を算出します。このδの値には、下層階から累積する回転による変形δmが含まれています。1次モードを仮定して等価せん断型のモデルを作る場合、図のように下層から上層に上がるにつれて回転量が累積し、各階の層間変形に占める割合が大きくなってきます。
一方、右のような2次モードで応答した場合には、途中の層で回転方向が反転するため1次モードほど回転による変形の累積は起こりません。しかし、等価せん断型モデルでは、変形性状にかかわらず、左図のように回転が累積すると仮定して算出したばね値を用いることになります。そのため、等価せん断型では2次モード以降の外力分布が作用した場合(右図の変形状態)には実際の曲げ変形よりも大きな曲げ変形を想定する、つまり剛性を小さく、固有周期を長く評価することになります。
一方、等価曲げせん断型はせん断剛性と曲げ剛性を分離することで、2次以降のモードにおいても外力分布形の変化に追従して層剛性をより精度高く評価することになります。
これが、等価曲げせん断型が必要な理由です。
実際の各モデルによる固有周期
立体モデルによる固有周期が正解として、各モデルの固有周期がどのくらい差が生じるか建物モデルで確認してみました。対象としたのは、20階建てRC造モデルです。| 等価せん断 | 等価曲げせん断 | 立体モデル | |
| 1次固有周期(s) | 1.585 | 1.579 | 1.568 |
| 2次固有周期(s) | 0.574 | 0.511 | 0.502 |
まとめ
- 等価曲げせん断は塔状比が大きくなり、建物の曲げ変形の影響が大きいと考えられる場合に重要となる。
- 等価せん断と等価曲げせん断では、2次以降のモードで差が生じ、等価せん断の固有周期 > 等価曲げせん断の固有周期となる。
関連するソフト RESP-D,RESP-MX
採用情報
構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。 採用HPはこちら→https://www.kke.co.jp/recruit/