はじめての同調型ダンパー

制振部材であるダンパーとしては、速度依存型ダンパー（オイルダンパーや粘性ダンパー）や履歴型ダンパー（座屈拘束ブレース）などが有名ですが、中には同調型ダンパーとよばれる特徴的なダンパーも存在します。今回はその同調型ダンパーの性質を応答解析結果から考えます。

1. 同調型ダンパー概要

まず、速度依存型ダンパー、履歴型ダンパー、同調型ダンパーそれぞれの建物の応答低減原理を簡単に整理したいと思います。

ダンパーの種類	応答低減原理
速度依存型ダンパー	速度に依存して発生する減衰力によって振動エネルギーを吸収する。
履歴型ダンパー	履歴エネルギーによってエネルギーを吸収する。
同調型ダンパー	補助的な質量を付加することで建物の特定の周期に対する応答を低減する。

同調型ダンパーは「動吸振器」とも呼ばれ、他のダンパーとの最大の違いは、特定の周期帯の応答を減少させることができる点です。

同調型ダンパーの具体的な例としては、TMD（チューンドマスダンパー）、iRDTダンパー、スロッシングダンパー、AMD（アクティブマスダンパー）などが挙げられます。実際には、付加質量を与えるだけでなく、速度依存型ダンパーと組み合わせて使用されることが一般的です。

2. 解析結果からみた同調型ダンパーの性質

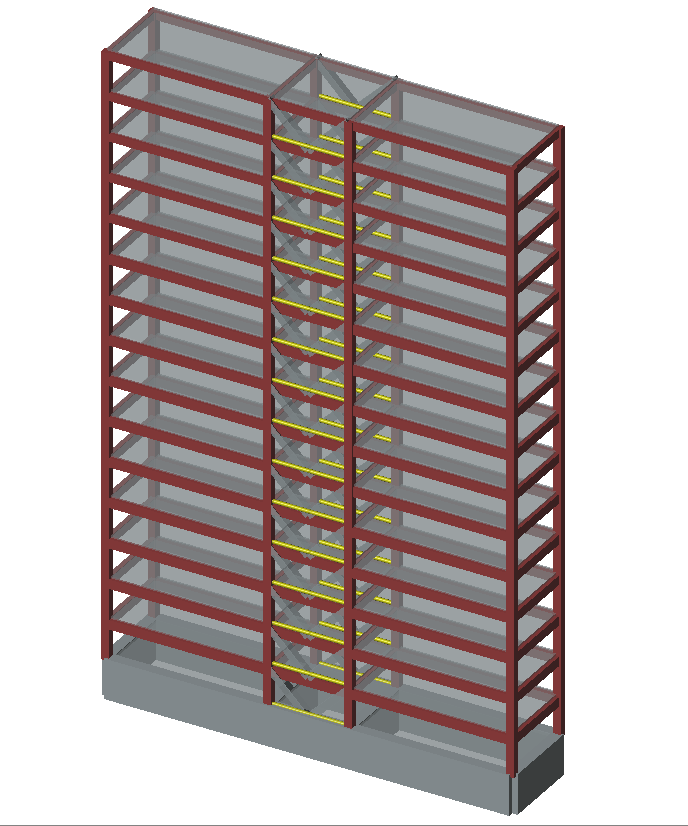
同調型ダンパーの性質を実際のモデルの解析結果から考察してみたいと思います。RESP-Dにより地上15階の建物モデルを作成し、⻑⼿⽅向にシアリンク型iRDTダンパーを配置することとします。

建物モデル
地上15建て（各構造階⾼︓3000mm）
S造
X⽅向スパン（⻑⼿⽅向）︓30000mm、Y⽅向スパン（短辺⽅向）︓6000mm
X⽅向⼀次固有周期[sec]︓1.08、Y⽅向⼀次固有周期︓1.35
図中の⻩⾊で⽰される部材がiRDTダンパー。

調査するもの
同調型ダンパーの性質を調べるうえで、横軸を固有周期比（一次固有周期に対する比）、縦軸を⼊⼒地震動に対する屋上階の応答加速度の伝達関数としたグラフを書いてみます。これにより特定の周期に対してどの程度の応答低減効果があるかを調査することができます。
⼊⼒地震動に対する屋上階の応答加速度の伝達関数は以下のステップで算出します。

RESP-F3Tにて時刻歴応答解析を実施し、最上層の応答加速度時刻歴を出⼒する。
RESP-F3Tにて⼊⼒地震動と最上層の応答加速度時刻歴をフーリエ変換し、周期の関数に変換する。（フーリエスペクトルを得る。）
2で得た⼆つのフーリエスペクトルをそれぞれ対応する周期ごとに除算することで、伝達関数を得る。（最上層の応答加速度時刻歴のフーリエスペクトル / ⼊⼒地震動のフーリエスペクトル）

2.1 iRDTダンパーの最適性能

同調型ダンパーとしてiRDTダンパーを用いることとします。下表に示したiRDTダンパーの性能を基本性能とし、以降の解析ではこの基本性能から剛性や減衰係数を変化させることとします。

このダンパー性能は定点理論を用いて決定しています。定点理論とは横軸を固有周期比、縦軸を伝達関数とするグラフにおいて、減衰係数を変化させても必ず2つの定点を通るという理論になります。（次節では解析結果からこの理論を体験してみます。）この理論を用いることで応答低減効果が最大になる減衰係数を求めることができます。参考文献[1]に定点理論による設計法が示されています。

ここで簡単にiRDTの直列剛性の導出方法について説明します。定点理論により最適性能を算出した後、ブレースによる水平剛性分を差し引いて、iRDTダンパーの剛性を計算する必要があります。
モデル図から分かる通り、iRDTダンパーはシアリンク型に配置されているため、ブレース2本分とダンパー直列剛性2本分の剛性を考慮します。

まず、ブレース1本分の剛性を $ K_{br} $ とすると、

$$\large K_{br} = \frac{E \cdot A}{L} $$
（A：断面積、L：材長、E：ヤング率）

ブレース1本分水平の剛性を $ K_{brh} $ とすると、
$$\large K_{brh} = K_{br} \cdot \cos^2 \frac{\pi}{4} $$

最適剛性を $ K_{opt} $ とし、iRDTダンパーの剛性を $ K_{irdt} $ とすると、

$$\large \frac{1}{K_{opt}} = \frac{1}{2 \cdot K_{brh}} + \frac{1}{2 \cdot K_{irdt}} $$

の関係が成立します。ここから定点理論により算出したiRDTダンパーの最適剛性と、ブレースの水平剛性を利用して $ K_{irdt} $ が算出できます。

2.1 減衰を変化させる（定点理論の観測）

iRDTダンパーの減衰性能を変化させた時の伝達関数を下図に示します。また凡例と解析条件の対応も合わせて下表に示しました。地震波形は告示波（神戸L2）を用いて、X方向（長手方向）に入力しています。

凡例	解析条件
irdt_c_0	iRDTダンパーを配置しない
irdt_c_0.25	iRDTダンパーの減衰係数が基本性能の0.25倍
irdt_c_0.5	iRDTダンパーの減衰係数が基本性能の0.5倍
irdt_c_1	iRDTダンパーの減衰係数が基本性能の値と同じ
irdt_c_2	iRDTダンパーの減衰係数が基本性能の2倍
irdt_c_4	iRDTダンパーの減衰係数が基本性能の4倍

特徴1：固有周期付近のピーク

周期が1.1秒前後にて、irdt_c_0（iRDTダンパーを外したモデル）がピークとなっています。これはX⽅向の⼀次固有周期（1.08秒）に対応しているとためだと推察されます。

特徴2：定点理論

グラフを見ると、iRDTダンパーを配置した場合の伝達関数のグラフは常に2点を通ることが分かります。（0.9秒付近と1.1秒付近でirdtを配置した場合の伝達関数のグラフが同じ点を通っています。）これは定点理論と呼ばれる現象になり、同調型ダンパーの減衰性能を変化させても伝達関数のグラフは必ず2点を通ることが証明されています。この性質を用いることで、同調型ダンパーの性能を最適化することもできます。
irdt_c_0（iRDTダンパーを外したモデル）については定点からやや逸脱するグラフとなっていますが、これはiRDTダンパーを外したことにより周辺剛性が考慮されなくなったことによる影響だと考えられます。

2.2 剛性を変化させる

iRDTダンパーの剛性を変化させた時の伝達関数を下図に示します。凡例と解析条件の対応も下表に示しました。地震波形は告示波（神戸L2）を、入力方向はX方向（長手方向）としています。

凡例	解析条件
irdt_0	iRDTダンパーを配置しない
irdt_0.25	iRDTダンパーの剛性が基本性能の0.25倍
irdt_0.5	iRDTダンパーの剛性が基本性能の0.5倍
irdt_1	iRDTダンパーの剛性が基本性能の値と同じ
irdt_2	iRDTダンパーの剛性が基本性能の2倍
irdt_4	iRDTダンパーの剛性が基本性能の4倍

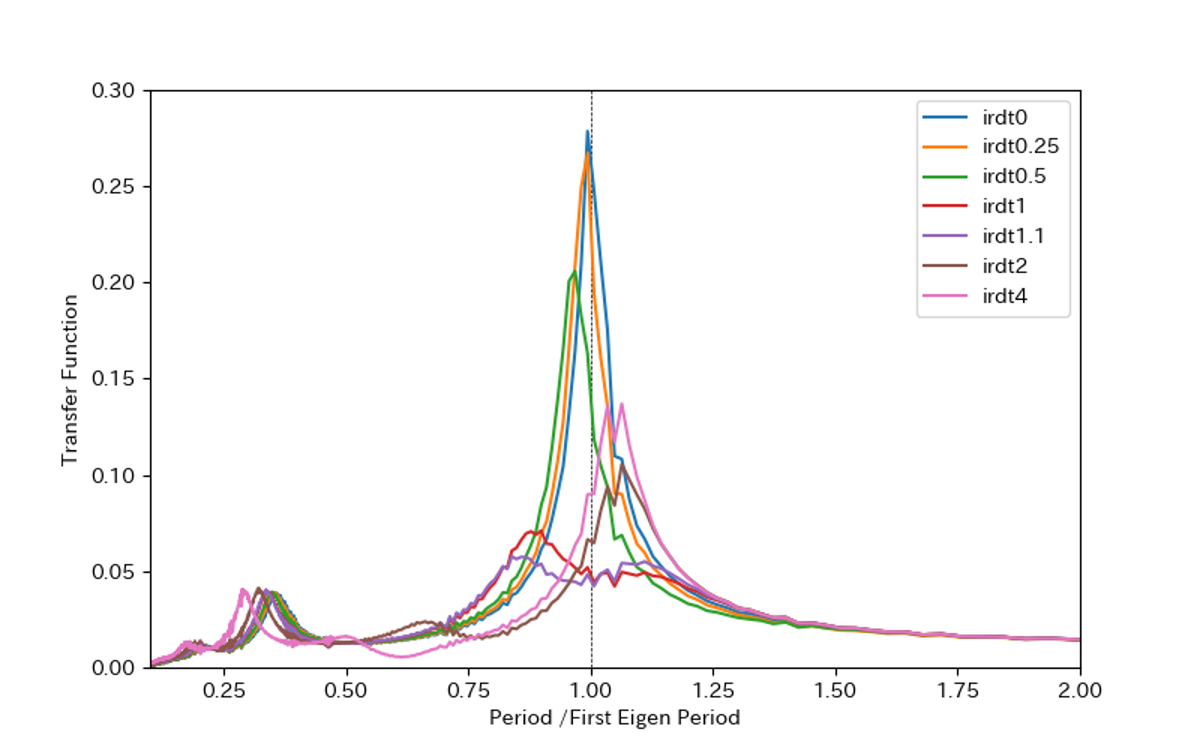
特徴：剛性の増減による応答低減効果の変化量の違い

irdt0.25（irdtダンパーの剛性を1/4倍）とirdt4（irdtダンパーの剛性を4倍）を⽐較すると、irdt0.25の⽅が伝達関数のピークが約2倍程度⼤きいことが読み取れます。つまり、最適剛性から低下させる⽅が増加させるよりも最適な性能からの逸脱が大きくなる傾向にあることが分かります。設計値である最適剛性から実際の剛性がずれた場合の挙動を考えると、やや大きめに剛性の値を設定したほうが応答低減効果の劣化の程度が軽微で済むということを指しています。これは既往の研究結果[2]とも整合しています。

まとめ

iRDTダンパーを用いて同調型ダンパーの性質を調査しました。減衰性能を変化させることで、定点理論を再現できることを確認しました。また、剛性を変化させることで、剛性の増減によって応答低減効果に差が生じることを確認できました。

参考文献

1: 麻美.細川,"主系の減衰を考慮した動吸振器の設計式について（第2報, 定点理論に基づく設計法）", 日本機械学会論文集,1995.3
2: 宮崎.他,"設計諸元変動を考慮した同調粘性マスダンパー制振システム地震時応答のロバスト性",日本建築学会大会講演論文集, 2013.8

【構造解析TIPS】はじめての同調型ダンパー

はじめての同調型ダンパー

目次

1. 同調型ダンパー概要