上下動係数を考慮した免震部材軸力の検討
免震部材の軸力検討において、支承材に引き抜きが発生し、引張による剛性低下を考慮したいときがあります。その場合、上下動をどのように考慮するかが課題となります。
なぜなら、引き抜きが発生しなければ、発生した軸力に対して後から引張側、圧縮側に上下動による軸力を加算すればよいだけですが、剛性低下が生じる場合には単純に応力として加算するだけでは剛性低下の影響を考慮した応力再配分が行われないためです。
そのため、テクニックとして、あらかじめ長期軸力を上下動係数分低減したり増加させたりしたうえで解析を行う、という方法が用いられます。これにより、上下動が作用した場合の引き抜きを模擬的に考慮しようというものです。
ですが、この方法の場合以下の欠点があります。
- 解析モデルを2つ作成する必要がある
- 圧縮側の検討の場合、隣接する支承材が引き抜けた場合の応力再配分が考慮されない
これらを解決するため、以下の記事では引張側に長期軸力を低減させつつ(初期応力を倍率で補正する)、後から上下動係数の2倍分を圧縮側の検討時に加算するという方法を考案しています。
NO.29 静的荷重増分解析結果を用いて免震支承材の引き抜き検討を行いたい
ただし、この方法はあまりよくみられるやり方ではないため、本記事で妥当性について検証を行いたいと思います。
検討は静的解析、動的解析それぞれで行います。
解析モデル
解析モデルは、引き抜きを検証するため4つの支承材からなり塔状比が非常に大きい極端な建物モデルを想定しました。支承材は天然ゴム系積層ゴムとしています。
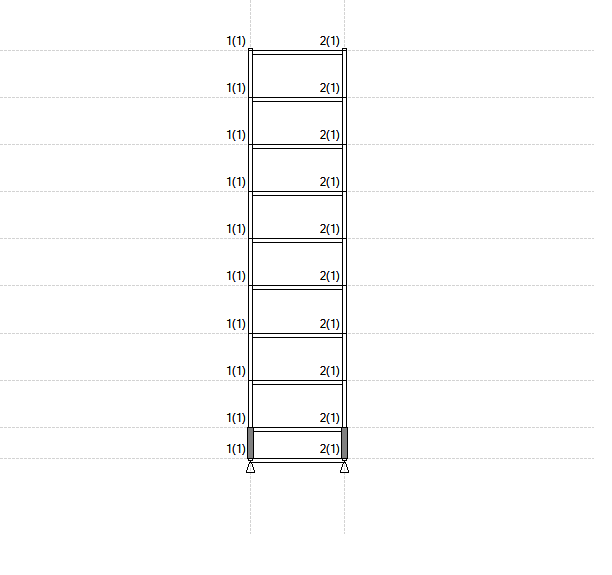
また、事前の上下動応答解析より、上下動係数は0.5G相当であることがわかりました。
以降、モデルは以下のように呼びます。
- 同時加振モデル(動的な水平・鉛直同時加振による、精算モデル)
- 同時加振(弾性)モデル(同時加振モデルに対して、免震支承材の軸剛性を弾性としたもの)
- ハイブリッドモデル(免震部材の初期応力を長期に対して0.5倍し、圧縮側軸力の検討時には0.5×2の上下動係数を加算するモデル)
- 引張側モデル(免震部材の初期応力を長期に対して0.5倍したモデル)
- 圧縮側モデル(免震部材の初期応力を長期に対して1.5倍したモデル)
免震部材の引張側の特性は、引張に入った直後から剛性低下率0.1となるように設定しました(同時加振(弾性)モデルを除く)。
減衰は、レーリー減衰として水平の1次周期(3.55秒、天然ゴム系積層ゴムのため歪には依存しない。)と上下の1次周期(0.09秒)で2%となるようにしました。
なお、入力する地震動は水平は周期3秒の正弦波、鉛直は周期0.1秒の正弦波を用いました。それぞれの最大加速度は、70gal,20galとしています。
解析結果は、以下の2つの観点で評価します。
- ハイブリッドモデルの妥当性。圧縮側モデル、引張側モデルと整合が取れるか。
- 同時加振モデルを正解とした場合の、各モデルの精度がどの程度か。
同時加振モデルの結果
まず、今回の検討の正解値となる、同時加振モデルの結果を示します。表は着目した支承材の、最大圧縮軸力および引張軸力です。

引張非線形を考慮しない弾性モデルのほうが、圧縮、引張軸力が大きくなっていることが確認できました。
この結果をベースに以降の検討と比較したいと思います。
静的解析による比較
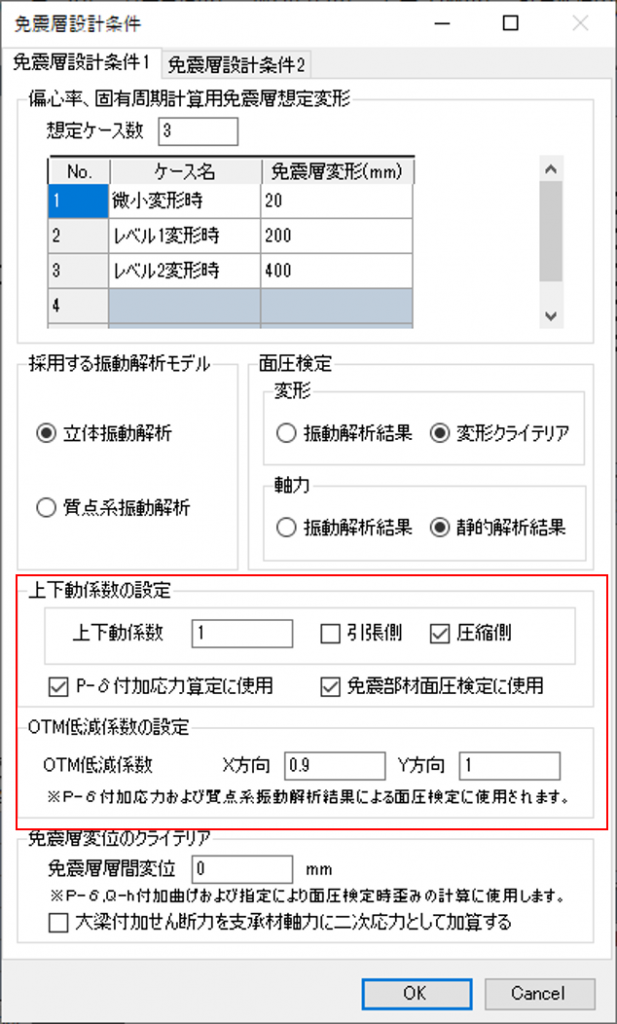
静的解析による検討では、免震層上のフロアレベルにおける転倒モーメントが同時加振モデルで発生した転倒モーメントと同程度になるように転倒モーメント低減比を設定して外力分布を定めたうえで、上下動係数を考慮した検討を行いました。
RESP-Dでは、免震層設計条件で設定できます。
上下動係数は0.5×2=1.0を圧縮側のみに作用させることとし、OTM低減係数は0.9としています。
結果を示します。(同時加振、同時加振(弾性)の結果は再掲となります。)

結果としては、引張側モデル、圧縮側モデルでも着目している方向の軸力に関してはハイブリッドモデルと同等の評価となりました。つまり、ハイブリッドモデル一つで引張側および圧縮側の検討を行える、という可能性が示されたということになります。一方、圧縮側モデルは引き抜きが発生しなくなるため、ハイブリッドモデルによる圧縮軸力に対して差が生じると予想しましたが、この影響は今回のモデルでは小さいという結果となりました。
ここで着目すべき点は、引張側・圧縮側・ハイブリッドモデルの軸力が、正解値として考えている、同時加振モデルに比べて全体的に大きくなっている点です。これは、仮定している上下動係数0.5Gが線形の上下動応答解析を行った結果から定めた値であるのに対し、同時加振モデルでは引き抜きが発生することにより上下動に対する剛性が変化し、実質的に上下動係数が低減したことが原因と考えられます。それは、引張側の非線形を非考慮とした解析(「同時加振(弾性)」)においてはよく一致する結果が得られたことからも裏付けられます。したがってこの乖離は、上下動係数の考慮方法の問題ではなく、上下動係数の設定に関する問題ということになります。
この結果からわかることとしては、通常は上下動係数を十分大きめにしておけば問題ないと思われますが、引き抜きが発生することにより上下動係数が励起されるような周期帯の地震動が入力される場合には注意が必要かもしれません。
動的解析の場合
つづいて、水平動を動的に入力し、上下動分を上下動係数として考慮しました。
結果を以下に示します。(同時加振、同時加振(弾性)の結果は再掲となります。)

傾向としては、静的同様に、ハイブリッドモデルでは一つのモデルで引張・圧縮側をよく評価できているといえます。
静的解析と比較すると、動的解析のほうが同時加振モデルとその他のモデルの結果の乖離が大きくなりました。この差異の要因は2点あると考えています。
- 上下動係数は、水平と鉛直の同時性を考慮すると実際には0.5Gは過大である(同時加振(弾性)と圧縮側の差異はこれに起因すると考えられる)
- ハイブリッドモデル、引張側モデルは同時加振モデルよりも引き抜きが早期に発生するため、振動モードが変化する
2つ目の要因については静的解析の場合でも発生はしますが、静的解析の場合は転倒モーメントと外力分布を合わせているのに対し、動的解析は転倒モーメント、外力分布にやや異なる傾向が見られたため、動的解析のみ差が大きくなったと考えられます。
まとめ
今回の検討の結果、あらかじめ初期応力を引張側、圧縮側に変動させた2つのモデルを作成して上下動を考慮した引き抜きを評価する代わりに、ハイブリッドモデル1つでも妥当な評価が行える可能性が示されました。
ただし、その場合でも実際に水平上下同時加振を行った場合との差異が生じることも確認されました。これについては、今後の課題としつつ、引き抜き検討の差異には留意しておくべき事象であると考えます。