2017年度建築学会大会梗概「材端剛塑性ばね法を適用した構造解析モデルに関する検討 その1 部材における検討」の内容を再編集したものです。
著者：角 友太郎, 鈴木 壮, 佐藤 克哉, 山根 義康
KeyWord：材端剛塑性ばね法, 弾塑性解析, 塑性ヒンジ, 鉄骨部材, 鉄筋コンクリート部材
1. はじめに
建築物の弾塑性解析を行う場合、梁要素の曲げ弾塑性特性を表現するために、材端に生じる塑性ヒンジを材端回転ばねによってモデル化する方法が広く用いられている。これは材端剛塑性ばね法と呼ばれ、部材が弾性範囲内では回転ばねを剛とし、塑性ヒンジが発生する段階で材端回転ばねを有効にして塑性化を表現する方法である。
本手法の概念を図1 に示す。材端に塑性域の変形を集中させることでモデルが明確となり、また計算が簡単になる、更には材端回転ばねに様々な履歴モデルを適用できるといった利点を有する。一方、本手法を採用する際に注意すべき点として、材端回転ばねの剛性を部材の曲げモーメント分布を予め仮定して決定するという点が挙げられる。部材の曲げモーメント分布により曲率分布は異なるため、曲率分布に伴い変化する回転角も本来であれば部材の曲げモーメント分布に依存する。そのため、曲げモーメント分布に合わせて材端回転ばねの剛性を変化させる方法が考えられるが、曲げモーメント分布は時々刻々変化するため、計算負荷の問題や履歴特性の扱いが難しくなることから、曲げモーメント分布を予め仮定する手法が採用される。
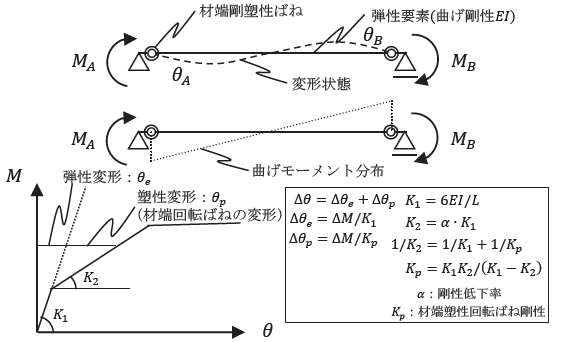図1 材端剛塑性ばねモデル法によるモデル化一般的には、水平荷重時の柱や梁の応力状態を考慮して部材中央に反曲点を持つ逆対称曲げモーメント分布を仮定して材端回転ばねの剛性を決定することが多い。しかし、材端がピンである場合や反曲点が部材中央から大きく離れる場合等、実際の応力状態が仮定と異なる場合、解析精度の低下に繋がることが懸念される。
そこで本報告では、材端剛塑性ばね法における材端回転ばね剛性算出時の曲げモーメント分布の仮定が解析結果に及ぼす影響について検討を行った結果を示す。
2. 部材における検討
2.1 検討方法
梁を想定した両端固定モデルに逆対称曲げモーメントを作用させた場合の𝑀 − 𝜃関係（端部節点位置の曲げモーメントと節点回転角）を2 つのモデルで比較する。解析モデルを図2 に、解析モデル諸元を表1 に示す。1 つは梁を1 つの要素でモデル化したもの（1 要素モデル）、もう1 つは梁を分割して2 つの要素でモデル化したもの（分割モデル）で、逆対称曲げモーメントの仮定は要素それぞれに適用されるため、分割モデルは梁全体としての逆対称曲げモーメントの仮定が成立しないことを想定したモデルである。立体3 次元モデル作成時には周辺部材の取り付きにより止むを得ず1 つの梁材を分割する場合がある。
図2 梁部材解析モデル
また、柱脚がピンとなるような柱や反曲点を持たない柱を想定して、図3 に示す片端固定他端ピンモデルに回転変形を作用させた場合の𝑀 − 𝜃関係（固定端の節点位置の曲げモーメントと節点回転角）を実際の曲げモーメント分布を仮定した場合と一般的な逆対称曲げモーメント分布を仮定した場合で比較を行う。
図3 柱部材解析モデル本検討において、せん断変形は考慮しない。復元力特性による違いを確認するため、検討はそれぞれ鉄骨（S）造部材と鉄筋コンクリート（RC）造部材に対して行い、履歴形状、塑性率、エネルギー吸収量に着目する。解析には(株)構造計画研究所の「RESP-F3T」を使用する。
2.2 検討結果
S 造部材の検討結果を図4、図5 に示す。S 造部材の場合、曲げモーメント分布の仮定が節点周りの𝑀 − 𝜃関係に及ぼす影響は小さいことがわかる。これは一般的に降伏後剛性に微小値を設定することが要因として考えられる。材端回転ばね剛性を算出する基となる剛性が曲げモーメント分布の違いにより本来のものと違ったとしても、1/1000 などの剛性低下率を考慮すると、塑性化後の剛性はほぼ零に近くなり、その影響度合いとしては小さくなる。
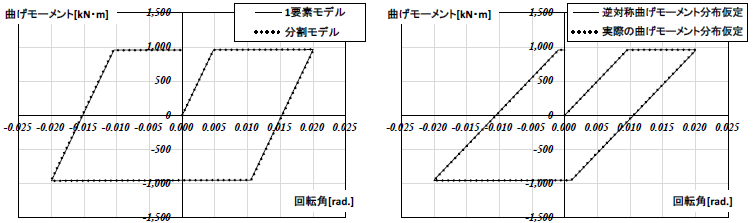図4 M − θ関係(S 梁) 図5 M − θ関係(S 柱)RC 造部材の検討結果を図6、図7 に示す。RC 造部材の場合、2 次剛性で顕著な差が生じており、材端回転ばね剛性算出時の曲げモーメント分布の仮定が節点周りの𝑀 − 𝜃関係に及ぼす影響は大きいことがわかる。これはひび割れ後の2 次剛性はある程度の大きさを有するため材端回転ばね剛性を算出する基となる剛性の違いが現れやすいことに起因する。
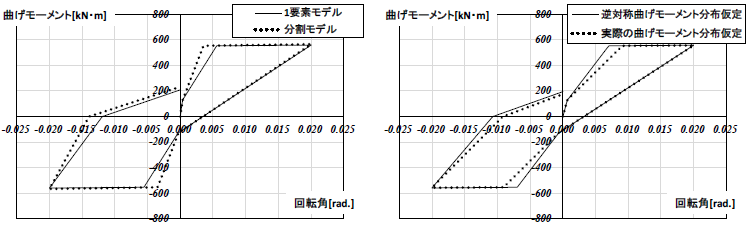図6 M − θ関係(RC 梁) 図7 M − θ関係(RC 柱)RC 梁解析モデルにおいて塑性率（D.F.）を変化させて1要素モデルと分割モデルの節点周りの𝑀 − 𝜃関係の差異を確認した結果を図8～図11 に示す。各塑性率は1 要素モデルの塑性率とする。これらの結果を図12 及び表2 にまとめる。塑性率に関しては大きくなるほどモデルによる差は大きくなり、1 要素モデルに対する分割モデルの塑性率は2.0 倍に漸近することがわかる。またエネルギーに関しては塑性率が大きくなるほどモデルによる差は小さくなり、比率が1.0 に漸近することがわかる。ここで、塑性率は部材の履歴から計算されることに注意が必要である。
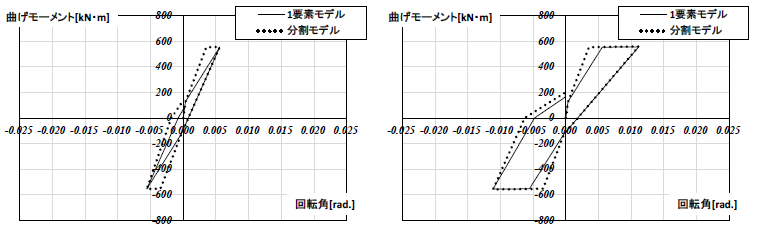図8 M − θ関係(RC 梁_D.F.=1.0) 図9 M − θ関係(RC 梁_D.F.=2.0)
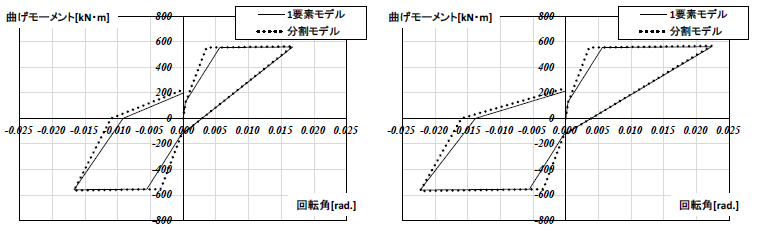図10 M − θ関係(RC 梁_D.F.=3.0) 図11 M − θ関係(RC 梁_D.F.=4.0)
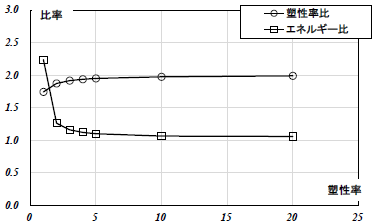図12 塑性率及びエネルギー比較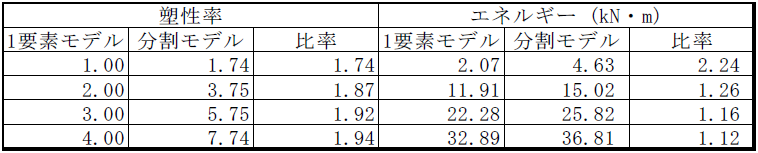
回転変形として与えた節点の回転角に対して、部材の履歴は分割モデル（2 分割）の場合、材長が半分になることに伴い初期剛性が2 倍になり、その線上を辿る。そのため、図13 に示すように横軸𝜃を材端回転角として部材の履歴を確認すると、S 造部材の場合にも弾性域で差異が確認される。つまり節点周りの釣り合いではなく部材に着目して塑性率やエネルギー吸収を考えると、部材分割の有無で評価が変わり、本検討から塑性率は最大で2 倍程度まで差が生じることがわかる。以上より、たとえ節点周りの釣り合いに及ぼす影響が小さくとも部材の評価に影響を及ぼす場合があることを確認した。
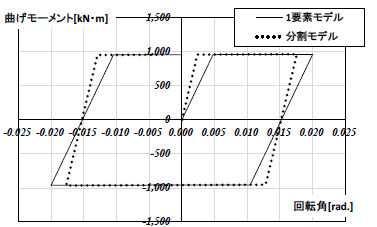図13 M − θ関係(S 梁_材端回転角)3. まとめ
その2 では立体架構において、材端剛塑性ばね法における材端回転ばね剛性算出時の曲げモーメント分布の仮定が解析結果に及ぼす影響について示す。
【参考文献】
1） 小谷俊介（2010）「鉄筋コンクリート造骨組の非線形解析」（第2 回中国耐震建築研修資料）
2） 鈴木壮,梁川幸盛ほか「材端剛塑性ばねモデルと適合するRC 部材のファイバーモデル化に関する検討」日本建築学会大会学術講演梗概集,2016