刺激係数は決まった値ではない
前回の記事で刺激係数は地動加速度の分布ベクトルを表現する時の固有ベクトルの係数であることを書きました。そのため、値が大きければその方向に寄与する度合いの大きさの指標の一つとみることができます。しかし、実は各モードの影響度合いは単純に刺激係数の絶対値の大きさだけで判断できません。その理由として刺激係数は絶対的に決まった確定値ではなく「固有ベクトルの基準化」という処理の方法で値が変わってしまうためです。
例えば、解析結果Aであるモードの刺激係数が1.5の場合に、解析結果Bであるモードの刺激係数が0.6の時、影響度合いを単純に数値だけで判断できない場合があります。
解析結果Aと解析結果Bが同じソフトなら良いですが、違うソフトの時は意味が異なる場合があります。
今回はその値が変わる様子を視覚的に説明していきます。
固有ベクトルの大きさについて
まずは、基準化を考える時に知らないといけない固有ベクトルの大きさについて説明します。以前から、固有ベクトルの大きさには意味がないという話をしてきました。この大きさに意味がないことを数値的に示してみます。次のような行列Aがあったとします。
$$
A = \left(\begin{array}{ccc} { 2.0 }& { -1.0 } & { 1.0 } \\\
{-1.0 }& { 2.0 } & {-1.0 } \\\
{ 1.0 }& { -1.0 } & { 3.0 } \end{array}\right)
$$
$$
\lambda = 4.414 \hspace{10pt} x = \left(\begin{array}{c} { 0.5 } \\\ {-0.5 } \\\ { 0.7071} \end{array}\right)
$$
$$
x = t \times \left(\begin{array}{c} { 0.5 } \\\ {-0.5 } \\\ { 0.7071} \end{array}\right)
$$
$$
A x = \lambda x
$$
$$
\left(\begin{array}{ccc} { 2.0 }& { -1.0 } & { 1.0 } \\\ {-1.0 }& { 2.0 } & {-1.0 } \\\ { 1.0 }& { -1.0 } & { 3.0 } \end{array}\right)
\left(\begin{array}{ccc} { 0.5 } \\\ {-0.5 } \\\ { 0.7071 } \end{array}\right)
=
\left(\begin{array}{ccc} { 2.207 } \\\ {-2.207} \\\ { 3.121 } \end{array}\right)
=
4.414 \times
\left(\begin{array}{ccc} { 0.5 } \\\ {-0.5 } \\\ { 0.7071 } \end{array}\right)
$$
$$
\left(\begin{array}{ccc} { 2.0 }& { -1.0 } & { 1.0 } \\\ {-1.0 }& { 2.0 } & {-1.0 } \\\ { 1.0 }& { -1.0 } & { 3.0 } \end{array}\right)
\left(\begin{array}{ccc} { 1.0 } \\\ {-1.0 } \\\ { 1.414 } \end{array}\right)
=
\left(\begin{array}{ccc} { 4.414 } \\\ {-4.414} \\\ { 6.243 } \end{array}\right)
=
4.414 \times
\left(\begin{array}{ccc} { 1.0 } \\\ { -1.0 } \\\ { 1.414 } \end{array}\right)
$$
固有ベクトルの基準化方法
大きさに意味がないのですが、プログラム内部で扱う時には離散的なデータで扱うため、前述のtはある大きさで決めることになります。プログラムでは固有ベクトルを計算した後に各次数ごとに大きさのルールを統一するために何らかの基準化の処理が入ります。代表的なものを記載します。- 全自由度のうち最大値を1.0にする
- 全自由度のうち最小値を1.0にする
- ノルム(ベクトルの大きさ)が1.0となるようにする
- モード質量が1.0となるようにする
刺激係数は基準化の影響を受ける
刺激係数はこの固有ベクトルの基準化の方法によって大きさが変わることを具体的な数値例で示します。次のような最大値を1.0にした固有ベクトルの刺激係数があったとします。$$
\left(\begin{array}{c} { 1.000} \\\ {1.000} \end{array}\right) =
1.20 \times \left(\begin{array}{c} { 1.000} \\\ {0.557} \end{array}\right) +
0.33 \times \left(\begin{array}{c} {-0.597} \\\ {1.000} \end{array}\right)
$$
$$
\left(\begin{array}{c} { 1.000} \\\ {1.000} \end{array}\right) =
0.668 \times \left(\begin{array}{c} { 1.794} \\\ {1.000} \end{array}\right)
-0.198 \times \left(\begin{array}{c} {1.000} \\\ {-1.676} \end{array}\right)
$$
図解!刺激係数
この基準化によって刺激係数が変わることを図で表してみます。前述の固有ベクトルで考えます。以前のブログからも固有ベクトルは基底として扱うのですが、それを図化するとこのようになります。固有ベクトルは大きさの係数があるので、大きさは任意に選べると考えると直線となります。このような表現を見慣れない方もいるかもしれませんが、じっくり観察して慣れてください。
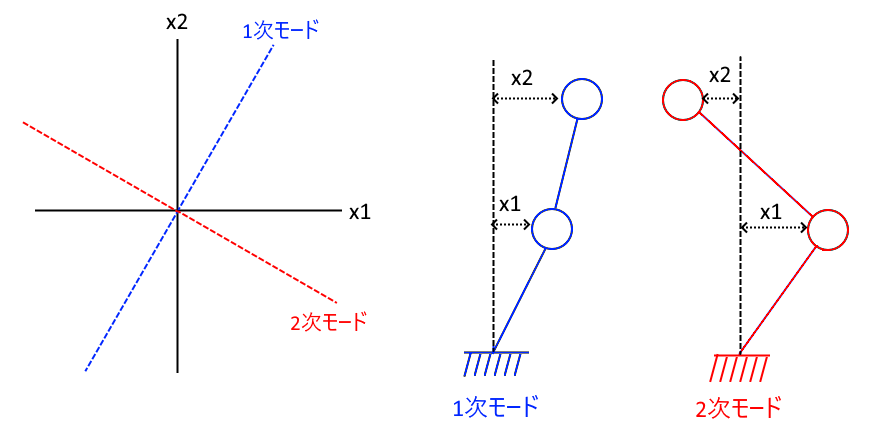
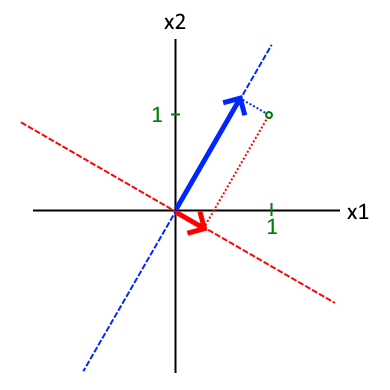
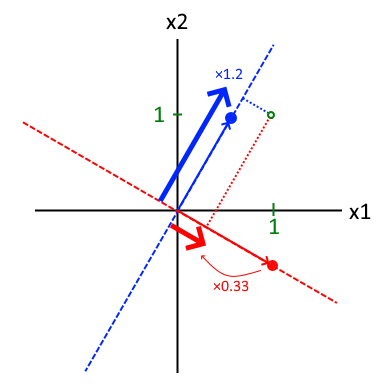
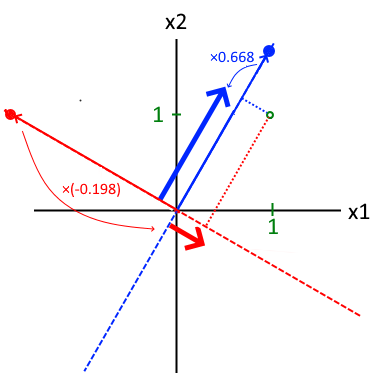
固有ベクトルは基準化によって 図中の● の位置が変わります。左図は最大値を1.0にしているので、前述の通りβ1=1.2、β2=0.33となります。右図は最小値を1.0にしてるのでβ1=0.668、β2=-0.198です。細線を太線に変化させる倍率として考えると見た目的にもの納得のいくものになっていると思います。
一方、刺激関数は?
このように刺激係数は固有ベクトルの基準化の影響を受けるという話をすると、「では、刺激関数は固有ベクトルをどのように基準化した時のものなの?」と質問を受けることがあります。結論から言うと、「どのように基準化しても刺激関数は変わらない」が答えです。前述の「最大値を1.0に基準化した絵」と 「最小値を1.0に基準化した絵」 を見比べてみると、太線(刺激関数)自体は変わっていません。刺激関数を表すための固有ベクトルが変わっているだけなので、最終的な刺激関数は不変の値となります。