固有値解析について
解析ソフトにおける固有値解析とはだいたい非減衰系の一般化固有値問題を指します。$$ \omega^2 M \boldsymbol{u} = K \boldsymbol{u} \tag{1}$$
固有周期は固有値を秒に単位変換したものとなります。
※固有値の単位は\( (\frac{rad}{秒})^2 \)です。
解析ソフトの結果で固有モード図を見ると、1次、2次などと書いてあったりします。いろんな次数の固有モード図を観察しているとどうやら、剛性が低い箇所だったり、質量が大きい箇所で大きく振れているように見えてきます。この様子を見て変位図と同じようなものと考えている人が多いように思えます。
座標系として考える
固有モード図の説明をいろいろ見ると相対的な比率とか振動形という説明がよくされているのですが、私は固有モード図は「座標系」と考えると自然かなと思っています。普段考えている座標系を回転して固有ベクトルを座標軸として考えるイメージです。詳細に説明するために図解します。 以下のような3自由度モデルを考えます。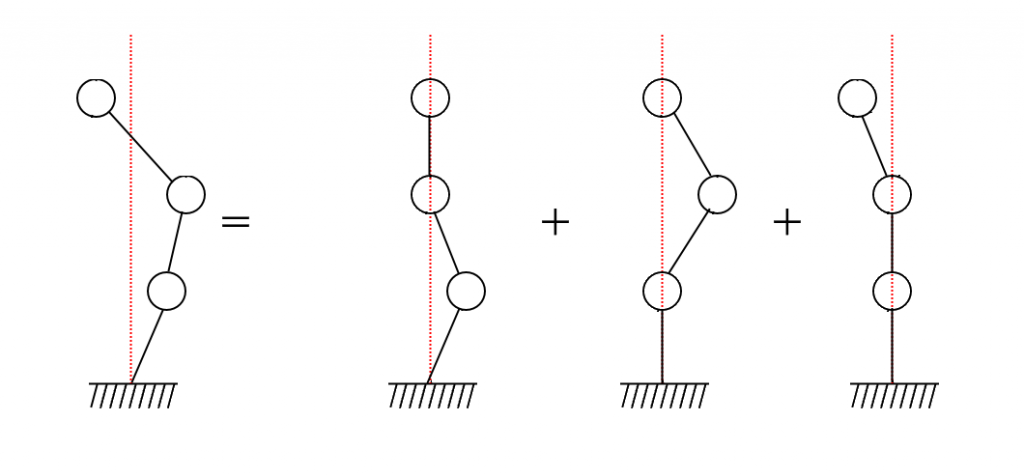
$$
\left(\begin{array}{c} {-0.750} \\\ {1.230} \\\ {0.850} \end{array}\right) =
\left(\begin{array}{c} { 0.000} \\\ {0.000} \\\ {0.850} \end{array}\right) +
\left(\begin{array}{c} { 0.000} \\\ {1.230} \\\ {0.000} \end{array}\right) +
\left(\begin{array}{c} {-0.750} \\\ {0.000} \\\ {0.000} \end{array}\right)
$$
上図の左辺の絵は3自由度系のある時の変位の状態を表しています。右辺はそれぞれの自由度のみが変位したときの絵で左辺は右辺の足し合わせと考えることができます。それぞれの絵で赤い点線の右側に変位する事を正、左側を負とします。一番上の節点のみ左側に変位してるので負となります。
次に右辺を各自由度の絵の変位量を1.0に基準化してみます。
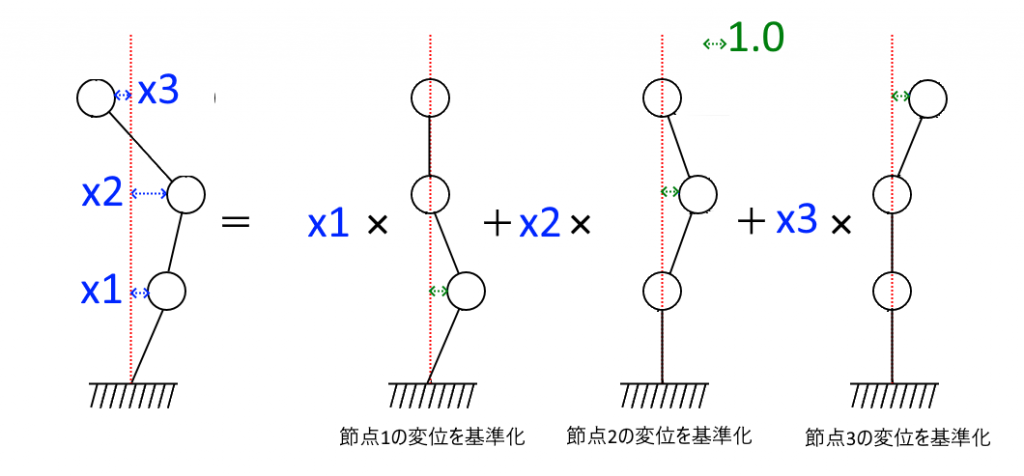
$$
\left(\begin{array}{c} {-0.750} \\\ {1.230} \\\ {0.850} \end{array}\right) =
\color{blue}{(0.850)} \times \left(\begin{array}{c} { 0.000} \\\ {0.000} \\\ \color{green}{1.000} \end{array}\right) +
\color{blue}{(1.230)} \times \left(\begin{array}{c} { 0.000} \\\ \color{green}{1.000} \\\ {0.000} \end{array}\right) +
\color{blue}{(-0.750)} \times \left(\begin{array}{c} \color{green}{1.000} \\\ {0.000} \\\ {0.000} \end{array}\right)
$$
次に「各節点の変位を基準化」した部分をこの3自由度系の固有ベクトルに変えてみます
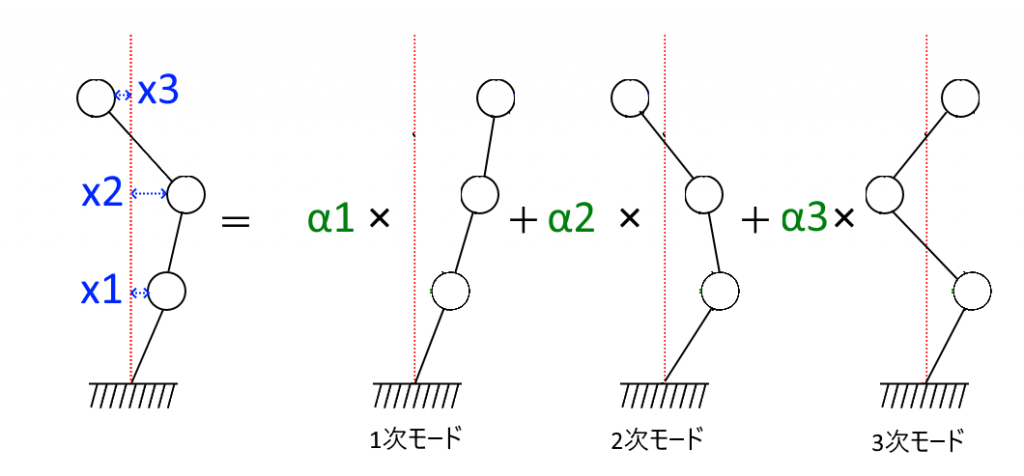
$$
\left(\begin{array}{c} { -0.750} \\\ {1.230} \\\ {0.850} \end{array}\right) =
\color{green}{{ (0.157)}} \times \left(\begin{array}{c} { 1.000} \\\ {0.750} \\\ {0.400} \end{array}\right) +
\color{green}{{ (1.040)}} \times \left(\begin{array}{c} {-0.750} \\\ {0.850} \\\ {1.000} \end{array}\right) +
\color{green}{{(-0.253)}} \times \left(\begin{array}{c} { 0.500} \\\ {-0.900} \\\ {1.000} \end{array}\right)
$$
今まで何の話をしていたか
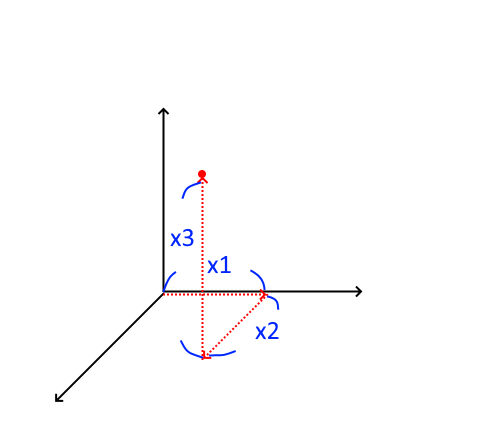
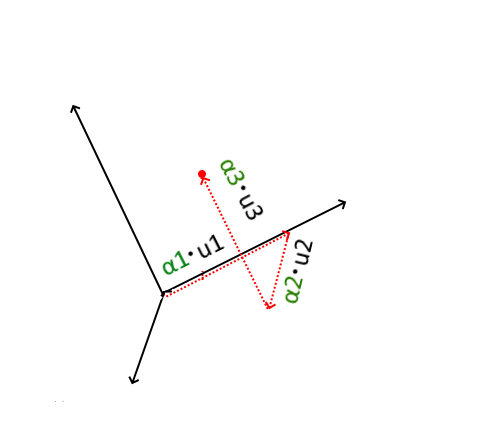
座標系の話をすると書いたのに何で絵の話になったか不思議に思う人もいるかもしれません。ここで絵での表現と座標系の関係性を説明します。絵で表現したような「基準となる形」があり、そこに倍数を掛けて表示をするという考え方は、XYZの座標系の表現と同じと考えることができます。 XYZの座標系の表現は以下の絵で、黒い基準線に倍率を掛けて赤い点線を作成し、それぞれを足すことで座標を表す事と同じです。ここが同一視できれば、上での説明が固有ベクトルを座標系と考えたということがわかるかと思います。
左右の図は原点からの同じ位置の座標を示していますが、黒い基準線の向きが異なるので、赤い点線の長さが変わっています。※まどろっこしく説明しましたが、座標変換です。
そして、変位図と固有モード図の違いですが、変位図はこの赤い点を表していますが、固有モード図のもとになる固有ベクトルは黒い基準線を表しています。
ちなみに、固有ベクトルが大きさに意味がないというのはこの黒い線の長さは任意に取れるというところからきています。この意味が分かればいろんなことが見えてくると思います。
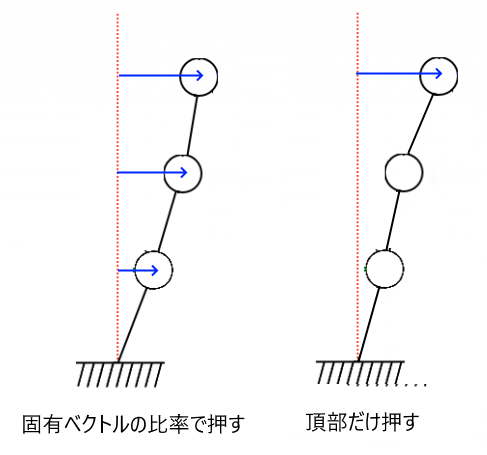
どんな座標系か
では、このように固有ベクトルを座標系として考えると何が良いのかを説明します。簡単のために質量マトリクスと剛性マトリクスの一般化固有値問題ではなく、単純に剛性マトリクスの標準固有値問題として考えます。$$ K \boldsymbol{u}= \lambda \boldsymbol{u} \tag{2} $$
Kは剛性マトリクス、λはその固有値、uはその固有ベクトルです。固有値問題はラフな言い方をすると「ある行列を使ってあるベクトルを線形変換したらベクトルの向きが変わらず、長さだけが変わる場合があり、その時の長さの変化率を固有値、ベクトルを固有ベクトルと呼ぶ」というものです。ここで、剛性方程式(3)で右辺の外力ベクトルが固有ベクトルに倍率βをかけたものだとします。
$$ K \boldsymbol{x} =\boldsymbol{F} \tag{3} $$
$$ \boldsymbol{F} = \beta \boldsymbol{u} \tag{4} $$
$$ K \boldsymbol{x} = \beta \boldsymbol{u} \tag{5} $$
(5)の連立方程式の解は(2)から次のようになります。$$ \boldsymbol{x} = \frac{\beta}{\lambda} \boldsymbol{u} \tag{6} $$
つまり、固有ベクトルの方向に加力をする時は、βという1つの変数で連立方程式を解くことができます。よく、「モード座標系では等価1自由度系と考えることができる」と言いますが、こう考えると意味が分かりやすいのではないでしょうか。
固有ベクトル、固有値がすべてわかっている場合、外力ベクトルは各固有ベクトルに倍率を掛けて足し合わせて表現することができるので、N自由度の剛性方程式は以下の手順で簡単に外力から変位を求めることができます。
- 外力ベクトルを固有ベクトルの線形和に分解する
- N個の(6)の方程式を解く
- 解いた結果で固有ベクトルをスカラー倍して、全部足し合わせると変位となる。
まとめ
少し抽象的でしたが、変位図が決まった座標系の中の座標を図化しているのに対して、固有モード図は座標系自体を図化していると考えることができます。そして、固有ベクトルを座標系として考えると等価1自由度系がイメージしやすくなります。また、この議論は線形範囲での話になります。非線形を考えると剛性マトリクスが変わるので、固有値解析やり直すことになります。
ちなみに、連立方程式を解くためにわざわざ固有値問題を解くのはむしろ手間になりますのでご注意を。