立体骨組構造静的弾性解析プログラム
今回は立体骨組構造静的弾性解析を行うプログラムのご紹介です。構造解析では具体的にどのようなことをしているか、を理解するための参考になれば幸いに思います。言語はPython3とします。以下のような立体骨組の解析結果（変位図）まで出力できるプログラムを作成してみます。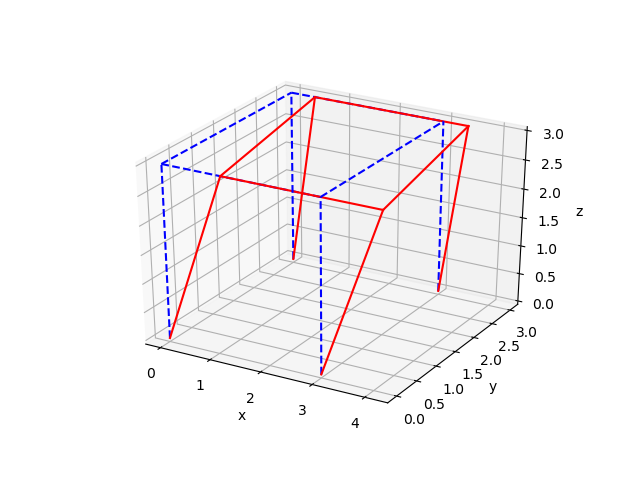
構造解析の概要
解析の流れ
大きくは以下のような流れになります。1. 各部材の要素剛性マトリクスを作成する
2. 要素剛性マトリクスから全体剛性マトリクスを作成する
3. 節点荷重ベクトルを作成する
4. 全体剛性マトリクスと節点荷重ベクトルから節点変位ベクトルを計算する
5. 節点変位ベクトルから要素変形を計算する
6. 要素変形と要素剛性マトリクスから要素応力を計算する
以降では、それぞれのステップについて少し詳しく見ていきます。
1. 各部材の要素剛性マトリクスを作成する
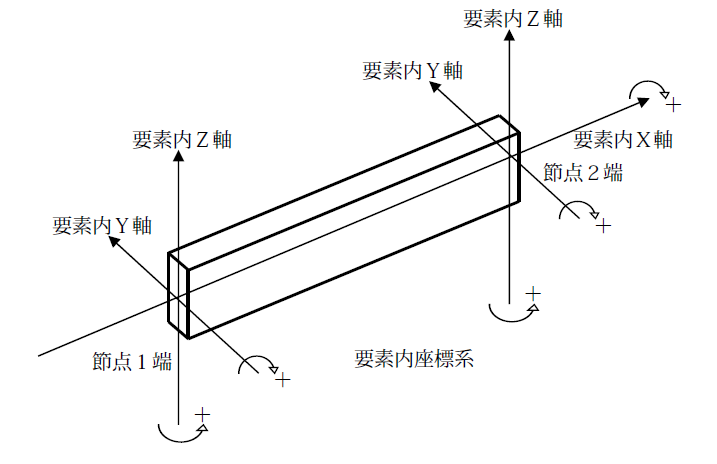
せん断変形を考慮しないベルヌーイ・オイラー梁を考える場合、梁要素の剛性マトリクスは以下のような対称マトリクスとして与えられます（ここでは、ねじり剛性も考えています）。要素の両端節点でそれぞれ6自由度ずつあるため、12×12のマトリクスになります。右側のベクトルは節点変位ベクトルを示します。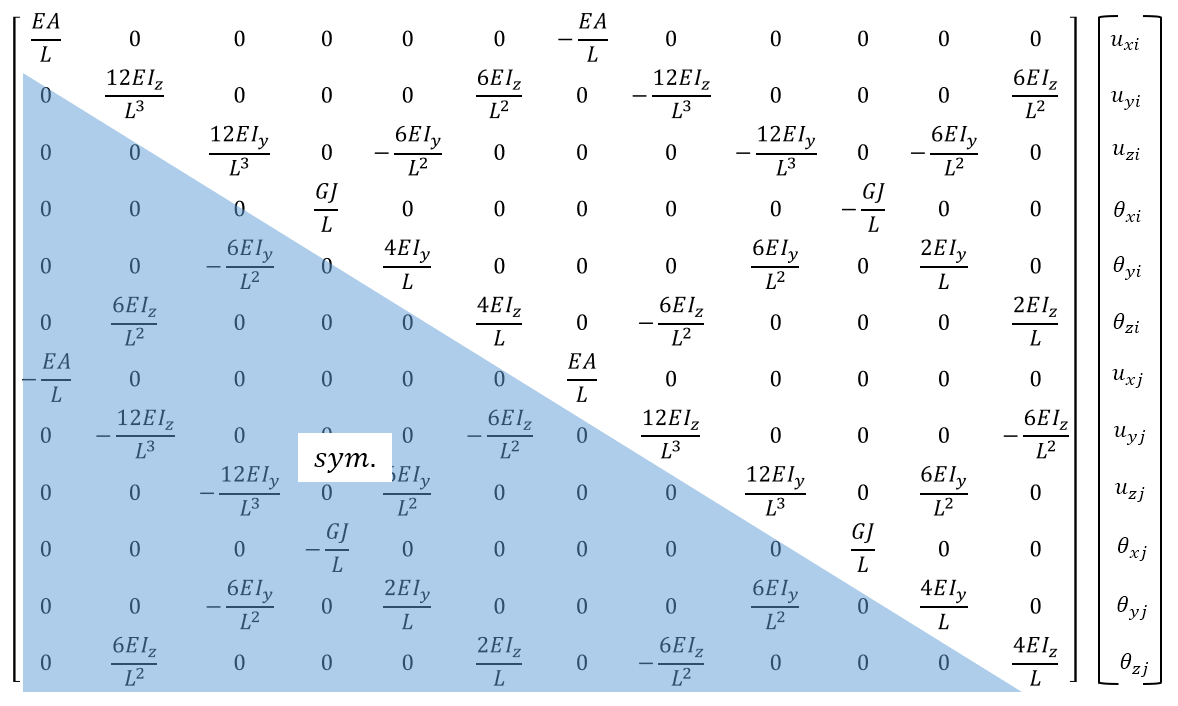
E：ヤング係数、I：断面二次モーメント、G：せん断弾性係数、J：ねじり定数
A：断面積、L：材長、u：変位、θ：回転角
2. 要素剛性マトリクスから全体剛性マトリクスを作成する
要素が複数あると、各要素が持つ座標系がばらばらであるため計算が難しそうです。そのため、統一した座標として全体座標系への変換を考えます。全体座標系はその空間に対する座標系を定義したものであり、この座標系の中に各要素が各要素座標系を持って存在します。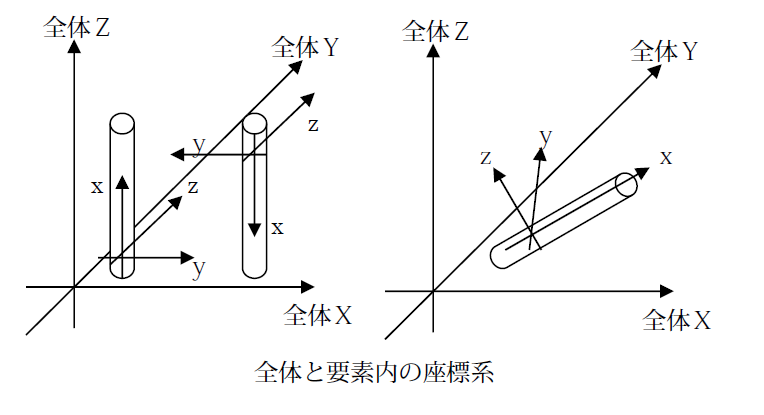
全体剛性マトリクスを作成するには、各要素について、要素剛性マトリクスの座標変換（要素⇒全体）と全体座標系に変換した要素剛性マトリクスを全体剛性マトリクスに反映する処理（ここではマップオンと呼ぶ）が必要になります。
座標変換マトリクス
座標変換マトリクスは以下の通りです。要素が直立（柱）の場合とそうでない場合とで変換マトリクスが変わるため注意が必要です（要素が直立の場合、lとmが零になるため、同じように計算できず、別途定式化されています。変換マトリクスの[3,2]の値がnではなく1なのは、常に要素座標系z軸を全体座標系Y軸に合わせているからです）。下図右下の[T]が最終的な座標変換マトリクスです。この座標変換マトリクスを要素剛性マトリクスに掛けることで要素剛性マトリクスを全体座標系に変換します。
X：X座標、Y：Y座標、Z：Z座標後ほど再掲しますが、プログラムでは以下のようになります。要素両端の節点から座標変換マトリクス(t)を求めて、要素剛性マトリクス(k)にそれを右から乗じます(kt)。その行列積(kt)に対して今度は座標変換マトリクスの逆行列を左から乗じます(tkt)。これで、要素剛性マトリクスを全体座標系に変換できます。
※ここでは、numpy（下のコードではnpと省略）というpythonの拡張モジュールを利用して行列積や逆行列を簡単に求めています。
def trans_elem_stiff_to_global(self):
"""
要素剛性を部材座標系から全体座標系に変換する
"""
t = utils.get_transform_matrix(self.NodeI, self.NodeJ)
kt = np.dot(self.Ke, t)
tkt = np.dot(np.linalg.inv(t), kt)
return tktマップオン
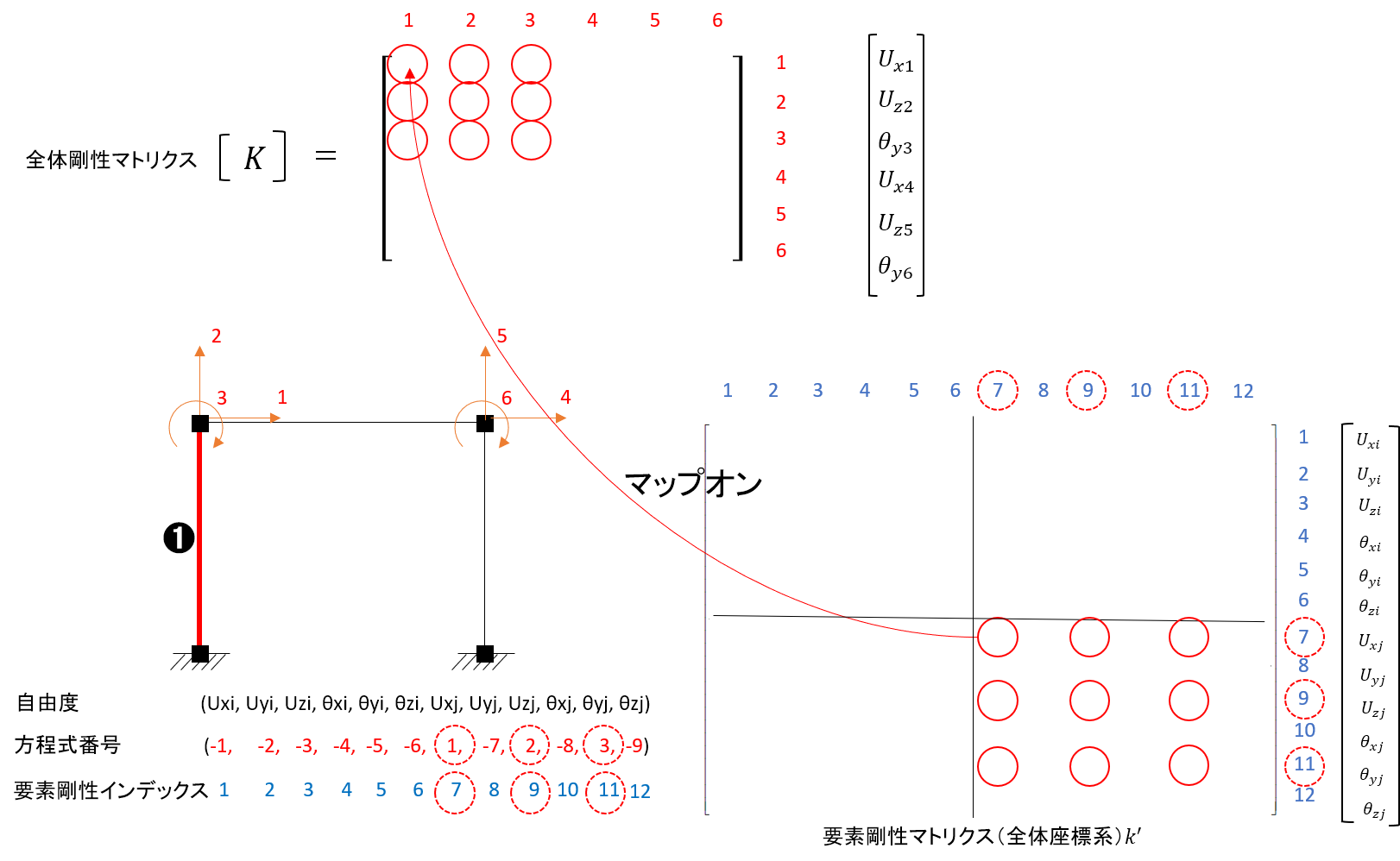
先ほど求めた要素剛性マトリクス（全体座標系）を全体剛性マトリクスに反映します。そのためにまず、当該要素の剛性がどの節点自由度に効くものかを対応付けるために方程式番号を用います。ここでは、解くべき自由度に対して正の値で番号付けをしておきます。また、解く必要の無い自由度（拘束自由度）に対しては負の値で番号付けすることにします。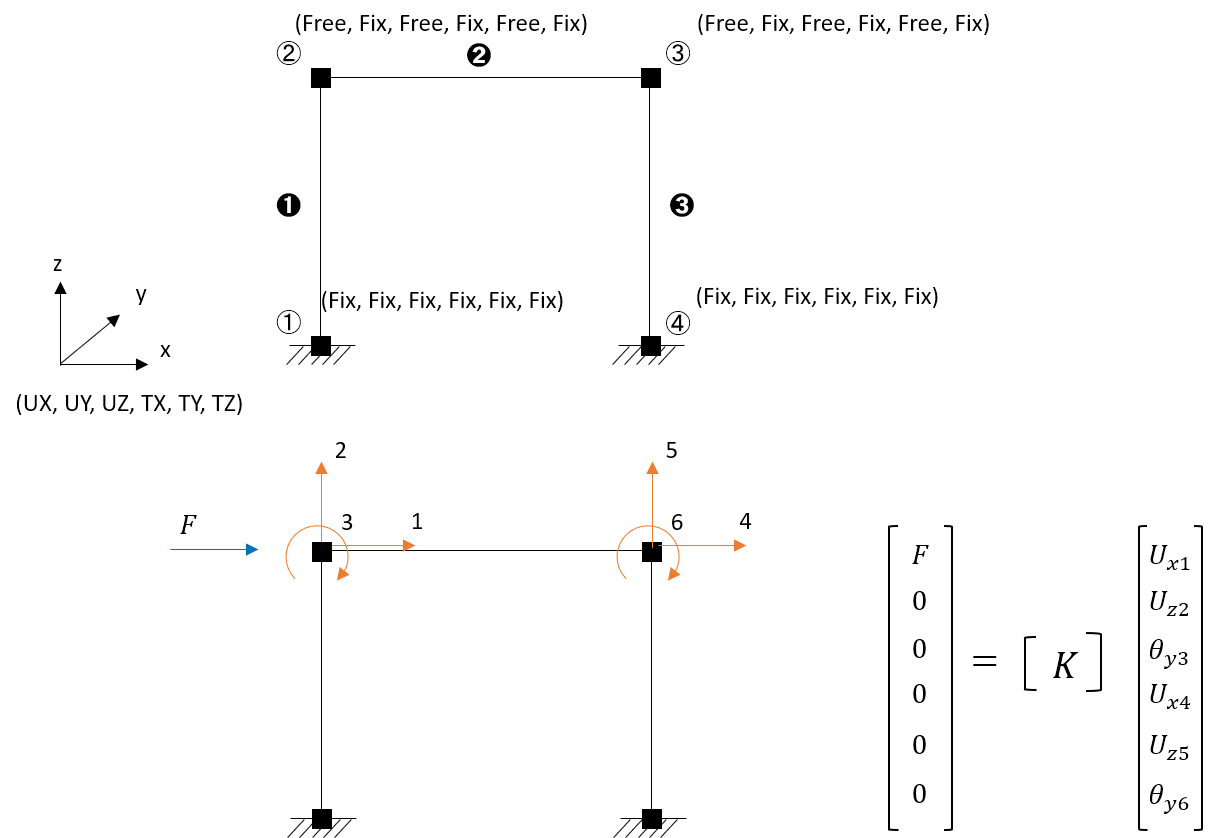
先ほど割り振った方程式番号に基づき、要素の剛性マトリクス（全体座標系に変換済みのもの）を全体剛性マトリクスに反映します。方程式番号を利用することで、解きたい自由度に対応した剛性を適切に反映することができます。下図では、簡単のために2次元で考えていますが、❶の部材について要素剛性マトリクスを全体剛性マトリクスの対応する位置に一つずつ反映しています。これを全部材について行うことで全体剛性マトリクスが完成します。
3. 節点荷重ベクトルを作成する
全体座標系での節点荷重ベクトルを作成します。下図（再掲）の赤枠で示したものが節点荷重ベクトルになります。節点荷重を全体座標系で与えている場合は座標変換が不要のため、先ほどと同様に方程式番号に基づいてマップオンするだけです。ベクトルであるため先のマトリクスよりもシンプルであり、節点自由度に対応する節点荷重を並べるだけです。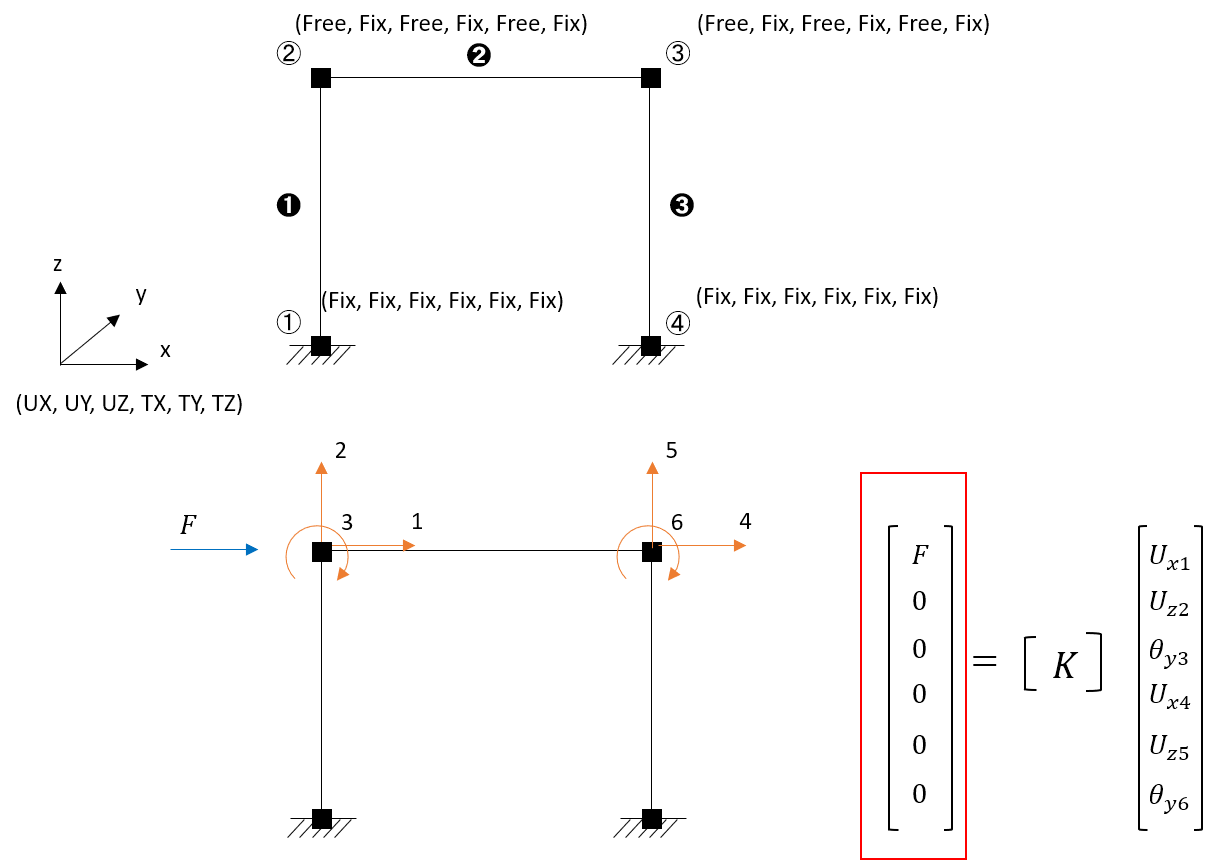
4. 全体剛性マトリクスと節点荷重ベクトルから節点変位ベクトルを計算する
節点変位ベクトルは全体剛性マトリクスの逆行列と節点荷重ベクトルを乗じることで求めます。今回のプログラムでは以下のようにnumpyの機能を利用して一行で終わりです。d = np.linalg.solve(ana_model.K, ana_model.F)5. 節点変位ベクトルから要素変形を計算する
節点荷重ベクトルを要素座標系に変換することで要素変形（ベクトル）を計算します。変換には再び座標変換マトリクスを用いています。以下該当部のコードです。# 節点の変位ベクトル（全体座標系）
disp_node_i = node_i.OutNode.Disp
disp_node_j = node_j.OutNode.Disp
disp = np.hstack((disp_node_i, disp_node_j))
# 節点の変位ベクトル（要素座標系）
t = utils.get_transform_matrix(node_i, node_j)
d = np.dot(t, disp)6. 要素変形と要素剛性マトリクスから要素応力を計算する
先ほど計算した要素変形（ベクトル）に要素剛性マトリクスを乗じて要素応力（ベクトル）を計算します。以下該当部のコード（先ほどの続き）です。# 要素応力f = k * d
k = beam.Ke
f = np.dot(k, d)プログラム概要
構成
今回は以下のような構成としてみました。FRAN（Frame Analysis）は今回のプログラムの名称です。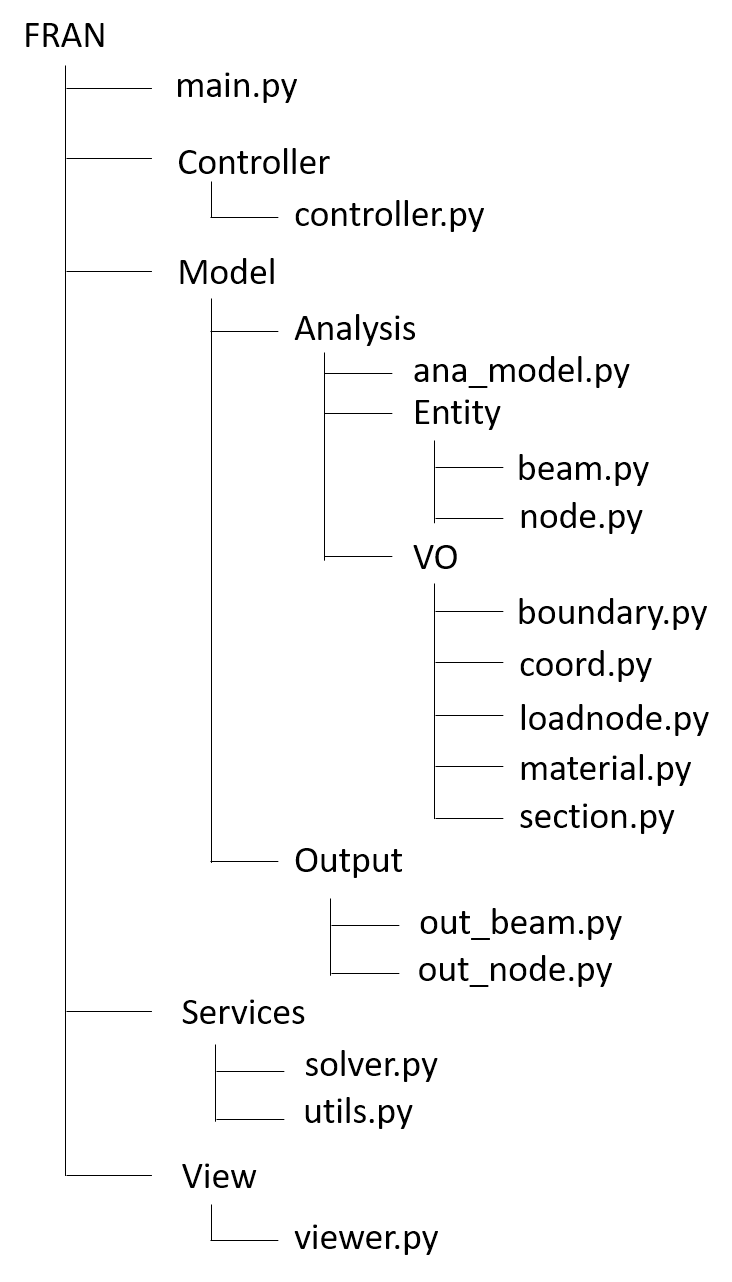
内容
main.py
プログラムのメイン部分です。プログラムの操作をControllerに任せるため、ここではControllerを呼んで実行するだけとしています。import sys, os
sys.path.append('./Controller')
from controller import Controller
if __name__ == "__main__":
ctl = Controller()
ctl.run()controller.py
メインから呼ばれるプログラムです。ここで解析部や結果描画部を呼んでいます。今回はサンプルモデルもここで作成しています。# coding:utf-8
import sys
import numpy as np
sys.path.append('./Model/Analysis/')
from ana_model import AnaModel
sys.path.append('./Model/Analysis/Entity')
from node import Node
from beam import Beam
sys.path.append('./Model/Analysis/VO')
from boundary import Boundary, BoundaryType
from section import Section
from material import Material
from loadnode import LoadNode
sys.path.append('./Services')
from solver import Solver
sys.path.append('./View')
from viewer import Viewer
class Controller:
"""
コントローラークラス
"""
def __init__(self):
"""
コンストラクタ
"""
self.Controller = self
def run(self):
"""
実行
"""
self.ana_model = self.get_sample_model(3)
Solver.solve(self.ana_model)
Viewer.view_frame(self.ana_model.Beams)
def get_sample_model(self, index):
"""
サンプルモデルの取得
"""
# 門形ラーメン3D（水平荷重）
node1 = Node('node1', 0.0, 0.0, 0.0) # 支点
node2 = Node('node2', 0.0, 0.0, 3.0)
node3 = Node('node3', 3.0, 0.0, 3.0)
node4 = Node('node4', 3.0, 0.0, 0.0) # 支点
node5 = Node('node5', 0.0, 3.0, 0.0) # 支点
node6 = Node('node6', 0.0, 3.0, 3.0)
node7 = Node('node7', 3.0, 3.0, 3.0)
node8 = Node('node8', 3.0, 3.0, 0.0) # 支点
boundary_pin = Boundary(BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Free, BoundaryType.Fix)
boundary_fix = Boundary(BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix, BoundaryType.Fix)
boundary_free = Boundary(BoundaryType.Free, BoundaryType.Fix, BoundaryType.Free, BoundaryType.Fix, BoundaryType.Free, BoundaryType.Fix)
node1.set_boundary(boundary_fix)
node2.set_boundary(boundary_free)
node3.set_boundary(boundary_free)
node4.set_boundary(boundary_fix)
node5.set_boundary(boundary_fix)
node6.set_boundary(boundary_free)
node7.set_boundary(boundary_free)
node8.set_boundary(boundary_fix)
material1 = Material(1.0, 1.0, 1.0)
section1 = Section(material1, 10000.0, 1.0, 1.0, 1.0, 1.0, 1.0)
beam1 = Beam('beam1', section1, node1, node2)
beam2 = Beam('beam2', section1, node2, node3)
beam3 = Beam('beam3', section1, node4, node3)
beam4 = Beam('beam1', section1, node5, node6)
beam5 = Beam('beam2', section1, node6, node7)
beam6 = Beam('beam3', section1, node8, node7)
beam7 = Beam('beam1', section1, node2, node6)
beam8 = Beam('beam2', section1, node3, node7)
loadnode = LoadNode(1.0, 0.0, 0.0, 0.0, 0.0, 0.0)
node2.set_load(loadnode)
list_node = [node1, node2, node3, node4, node5, node6, node7, node8]
list_beam = [beam1, beam2, beam3, beam4, beam5, beam6, beam7, beam8]
ana_model = AnaModel(list_node, list_beam)
return ana_modelana_model.py
解析モデルクラスです。すべての節点と梁要素をここで保持しています。また、行列計算するための方程式番号付け、全体剛性マトリクスの作成、全体荷重ベクトルの作成をしています。# coding:utf-8
import sys, os
import numpy as np
sys.path.append(os.path.join(os.getcwd(), 'Model/Analysis/Entity'))
from node import Node
from beam import Beam
sys.path.append(os.path.join(os.getcwd(), 'Model/Analysis/VO'))
from boundary import Boundary, BoundaryType
class AnaModel:
"""
解析モデルクラス
"""
def __init__(self, list_node:list, list_beam:list):
"""
コンストラクタ
"""
self.Nodes = list_node
self.Beams = list_beam
# 方程式番号
count_free = 0
count_fix = 0
for node in self.Nodes:
for index in range(6):
if node.get_boundary(index) == BoundaryType.Free:
# 自由 -> 正値
count_free += 1
node.set_equation_number(index, count_free - 1)
else:
# 固定 -> 負値
count_fix -= 1
node.set_equation_number(index, count_fix)
# 全体剛性マトリクス
self.K = np.zeros((count_free, count_free))
for beam in self.Beams:
beam.map_on_global_stiff(self.K)
# 全体荷重ベクトル
self.F = np.zeros(count_free)
for node in self.Nodes:
node.map_on_global_load(self.F)beam.py
梁要素クラスです。梁に関する情報（名前、I端節点、J端節点、部材長、要素剛性）を保持しています。また、要素剛性マトリクスの作成やその要素剛性マトリクスを全体剛性マトリクスに反映（マップオン）する関数もここで定義しています。# coding:utf-8
import sys
sys.path.append('.Model/Analysis/Entity')
sys.path.append('.Model/Analysis/VO')
from section import Section
from node import Node
import numpy as np
sys.path.append('.Model/Output')
from out_beam import OutBeam
sys.path.append('./Services')
import utils
class Beam:
"""
梁要素クラス
"""
def __init__(self, name:str, section:Section, nodeI:Node, nodeJ:Node):
"""
コンストラクタ
"""
self.Name = name
self.Section = section
self.NodeI = nodeI
self.NodeJ = nodeJ
self.Length = utils.get_length_between_two_node(nodeI, nodeJ)
self.Ke = self.get_elem_stiff()
def get_elem_stiff(self):
"""
要素剛性を取得する
"""
eA_per_L = self.Section.Material.E * self.Section.AX / self.Length
gJ_per_L = self.Section.Material.G * self.Section.IX / self.Length
eIy_per_L1 = self.Section.Material.E * self.Section.IY / self.Length
eIz_per_L1 = self.Section.Material.E * self.Section.IZ / self.Length
eIy_per_L2 = eIy_per_L1 / self.Length
eIz_per_L2 = eIz_per_L1 / self.Length
eIy_per_L3 = eIy_per_L2 / self.Length
eIz_per_L3 = eIz_per_L2 / self.Length
#0 #1 #2 #3 #4 #5 #6 #7 #8 #9 #10 #11
ke = ([ [ eA_per_L, 0.0, 0.0, 0.0, 0.0, 0.0, - eA_per_L, 0.0, 0.0, 0.0, 0.0, 0.0], # 0
[ 0.0, 12.0 * eIz_per_L3, 0.0, 0.0, 0.0, 6.0 * eIz_per_L2, 0.0, -12.0 * eIz_per_L3, 0.0, 0.0, 0.0, 6.0 * eIz_per_L2], # 1
[ 0.0, 0.0, 12.0 * eIy_per_L3, 0.0, -6.0 * eIy_per_L2, 0.0, 0.0, 0.0, -12.0 * eIy_per_L3, 0.0, -6.0 * eIy_per_L2, 0.0], # 2
[ 0.0, 0.0, 0.0, gJ_per_L, 0.0, 0.0, 0.0, 0.0, 0.0, - gJ_per_L, 0.0, 0.0], # 3
[ 0.0, 0.0, -6.0 * eIy_per_L2, 0.0, 4.0 * eIy_per_L1, 0.0, 0.0, 0.0, 6.0 * eIy_per_L2, 0.0, 2.0 * eIy_per_L1, 0.0], # 4
[ 0.0, 6.0 * eIz_per_L2, 0.0, 0.0, 0.0, 4.0 * eIz_per_L1, 0.0, -6.0 * eIz_per_L2, 0.0, 0.0, 0.0, 2.0 * eIz_per_L1], # 5
[ - eA_per_L, 0.0, 0.0, 0.0, 0.0, 0.0, eA_per_L, 0.0, 0.0, 0.0, 0.0, 0.0], # 6
[ 0.0, -12.0 * eIz_per_L3, 0.0, 0.0, 0.0, -6.0 * eIz_per_L2, 0.0, 12.0 * eIz_per_L3, 0.0, 0.0, 0.0, -6.0 * eIz_per_L2], # 7
[ 0.0, 0.0, -12.0 * eIy_per_L3, 0.0, 6.0 * eIy_per_L2, 0.0, 0.0, 0.0, 12.0 * eIy_per_L3, 0.0, 6.0 * eIy_per_L2, 0.0], # 8
[ 0.0, 0.0, 0.0, - gJ_per_L, 0.0, 0.0, 0.0, 0.0, 0.0, gJ_per_L, 0.0, 0.0], # 9
[ 0.0, 0.0, -6.0 * eIy_per_L2, 0.0, 2.0 * eIy_per_L1, 0.0, 0.0, 0.0, 6.0 * eIy_per_L2, 0.0, 4.0 * eIy_per_L1, 0.0], # 10
[ 0.0, 6.0 * eIz_per_L2, 0.0, 0.0, 0.0, 2.0 * eIz_per_L1, 0.0, -6.0 * eIz_per_L2, 0.0, 0.0, 0.0, 4.0 * eIz_per_L1] # 11
])
return ke
def trans_elem_stiff_to_global(self):
"""
要素剛性を部材座標系から全体座標系に変換する
"""
t = utils.get_transform_matrix(self.NodeI, self.NodeJ)
kt = np.dot(self.Ke, t)
tkt = np.dot(np.linalg.inv(t), kt)
return tkt
def map_on_global_stiff(self, matrix_global_stiffness):
"""
要素剛性を全体剛性にマップオンする
"""
tkt = self.trans_elem_stiff_to_global()
eq = self.NodeI.EquationNumber
eq.extend(self.NodeJ.EquationNumber)
for i_row in range(12):
e_row = eq[i_row]
if e_row < 0: continue
for i_col in range(12):
e_col = eq[i_col]
if e_col < 0: continue
matrix_global_stiffness[e_row, e_col] += tkt[i_row, i_col]
def set_out_beam(self, out_beam:OutBeam):
"""
結果出力用梁要素オブジェクトをセットする
"""
self.OutBeam = out_beamnode.py
節点クラスです。節点に関する情報（名前、座標、境界条件、方程式番号、荷重）を保持しています。また、節点荷重を全体荷重ベクトルに反映（マップオン）する関数もここで定義しています。# coding:utf-8
import sys, os
sys.path.append('Model/Analysis/VO')
from coord import Coord
from boundary import Boundary, BoundaryType
from loadnode import LoadNode
sys.path.append('Model/Output')
from out_node import OutNode
class Node:
"""
節点クラス
"""
def __init__(self, name:str, coordX:float, coordY:float, coordZ:float):
"""
コンストラクタ
"""
self.Name = name
self.Coord = Coord(coordX, coordY, coordZ)
self.Boundary = Boundary(BoundaryType.Free, BoundaryType.Free, BoundaryType.Free, BoundaryType.Free, BoundaryType.Free, BoundaryType.Free)
self.EquationNumber = [0, 0, 0, 0, 0, 0]
self.Load = [0.0, 0.0, 0.0, 0.0, 0.0, 0.0]
def set_boundary(self, boundary:Boundary):
"""
境界条件のセット
"""
self.Boundary = boundary
def set_equation_number(self, index:int, equation_number:int):
"""
方程式番号のセット
"""
self.EquationNumber[index] = equation_number
def set_load(self, load:LoadNode):
"""
節点荷重のセット
"""
self.Load = [load.LoadUX, load.LoadUY, load.LoadUZ, load.LoadTX, load.LoadTY, load.LoadTZ]
def get_boundary(self, index:int):
"""
境界条件の取得
"""
try:
if index == 0:
return self.Boundary.Ux
elif index == 1:
return self.Boundary.Uy
elif index == 2:
return self.Boundary.Uz
elif index == 3:
return self.Boundary.Tx
elif index == 4:
return self.Boundary.Ty
elif index == 5:
return self.Boundary.Tz
else:
raise Exception('不正なインデックス')
except Exception as e:
print(e)
sys.exit('エラーのためプログラムを終了します')
def map_on_global_load(self, load_vector:list):
"""
節点荷重を全体荷重にマップオンする
"""
for index in range(6):
e_num = self.EquationNumber[index]
if 0 <= e_num:
load_vector[e_num] += self.Load[index]
def set_out_node(self, out_node:OutNode):
"""
結果出力用節点オブジェクトをセットする
"""
self.OutNode = out_nodeboundary.py
境界条件クラスです。境界条件（6自由度）の情報を保持します。# coding:utf-8
from enum import Enum
class BoundaryType(Enum):
"""
境界条件列挙体
"""
Free = 'Free',
Fix = 'Fix'
class Boundary:
"""
境界条件クラス
"""
def __init__(self, ux:BoundaryType, uy:BoundaryType, uz:BoundaryType, tx:BoundaryType, ty:BoundaryType, tz:BoundaryType):
"""
コンストラクタ
"""
self.Ux = ux
self.Uy = uy
self.Uz = uz
self.Tx = tx
self.Ty = ty
self.Tz = tzcoord.py
座標クラスです。座標の情報を保持します。# coding:utf-8
class Coord:
"""
座標クラス
"""
def __init__(self, x:float, y:float, z:float):
"""
コンストラクタ
"""
self.X = x
self.Y = y
self.Z = zloadnode.py
節点荷重クラスです。節点荷重の情報を保持します。# coding:utf-8
class LoadNode:
"""
節点荷重クラス
"""
def __init__(self, loadUX:float, loadUY:float, loadUZ:float, loadTX:float, loadTY:float, loadTZ:float):
"""
コンストラクタ
"""
self.LoadUX = loadUX
self.LoadUY = loadUY
self.LoadUZ = loadUZ
self.LoadTX = loadTX
self.LoadTY = loadTY
self.LoadTZ = loadTZmaterial.py
材料クラスです。ヤング係数E、せん断弾性係数G、ポアソン比pを保持します。（※今回のプログラムは実際にはポアソン比は使っていません。）# coding:utf-8
class Material:
"""
材料クラス
"""
def __init__(self, e:float, g:float, p:float):
"""
コンストラクタ
"""
self.E = e
self.G = g
self.P = psection.py
断面クラスです。断面性能（断面積、断面2次モーメント）を保持します。# coding:utf-8
from material import Material
class Section:
"""
断面クラス
"""
def __init__(self, material:Material, ax:float, ay:float, az:float, ix:float, iy:float, iz:float):
"""
コンストラクタ
"""
self.Material = material
self.AX = ax
self.AY = ay
self.AZ = az
self.IX = ix
self.IY = iy
self.IZ = izout_beam.py
梁要素結果クラスです。今回は応力のみ保持します。# coding:utf-8
class OutBeam:
"""
梁要素結果クラス
"""
def set_stress(self, stress):
"""
コンストラクタ
"""
self.Stress = stressout_node.py
節点結果クラスです。節点変位を保持します。# coding:utf-8
class OutNode:
"""
節点結果クラス
"""
def set_disp(self, disp):
"""
コンストラクタ
"""
self.Disp = dispsolver.py
計算部です。全体剛性マトリクスと全体荷重ベクトルから節点変位を計算して、その変位から求まる要素変形から要素応力を計算します。変位図だけの出力であれば、節点変位だけ求めれば十分ですが、今回は要素応力も求めてファイル出力しています。# coding:utf-8
import os, sys, csv
import numpy as np
sys.path.append('./Model/Analysis/')
from ana_model import AnaModel
sys.path.append('./Model/Output')
from out_node import OutNode
from out_beam import OutBeam
import utils
sys.path.append('./Model/Analysis/VO')
from boundary import Boundary, BoundaryType
class Solver:
@staticmethod
def solve(ana_model):
"""
計算実行
"""
# 計算
calc_node_disp(ana_model)
calc_beam_stress(ana_model)
# 出力
output_result(ana_model)
def calc_node_disp(ana_model):
"""
節点変位を計算する
"""
d = np.linalg.solve(ana_model.K, ana_model.F)
# 節点変位を結果用オブジェクトにセット
for node in ana_model.Nodes:
out_node = OutNode()
size = 6
disp = np.zeros(size)
for index in range(size):
eq = node.EquationNumber[index]
if eq < 0:
disp[index] = 0.0
else:
disp[index] = d[eq]
out_node.set_disp(disp)
node.set_out_node(out_node)
def calc_beam_stress(ana_model):
"""
要素応力を計算する
"""
for beam in ana_model.Beams:
out_beam = OutBeam()
node_i = beam.NodeI
node_j = beam.NodeJ
# 節点の変位ベクトル（全体座標系）
disp_node_i = node_i.OutNode.Disp
disp_node_j = node_j.OutNode.Disp
disp = np.hstack((disp_node_i, disp_node_j))
# 節点の変位ベクトル（要素座標系）
t = utils.get_transform_matrix(node_i, node_j)
d = np.dot(t, disp)
# 要素応力f = k * d
k = beam.Ke
f = np.dot(k, d)
# 要素応力を結果用オブジェクトにセット
out_beam.set_stress(f)
beam.set_out_beam(out_beam)
def check_directory(path):
"""
フォルダの存在チェック
(無い場合は新規作成する)
"""
file_path = os.path.dirname(path)
if not os.path.exists(file_path):
os.makedirs(file_path)
def output_result(ana_model):
"""
解析結果を出力する
"""
out_file_path = 'Result/result.csv'
check_directory(out_file_path)
lines = []
# 節点変位
lines.append('*Node\n')
lines.append('Name,UX,UY,UZ,TX,TY,TZ\n')
for node in ana_model.Nodes:
tmp = []
tmp.append(node.Name)
disp = map(str, node.OutNode.Disp)
tmp.extend(disp)
tmp.append('\n')
line = ','.join(tmp)
lines.append(line)
lines.append('\n')
# 梁要素応力
lines.append('*Beam\n')
lines.append('Name,UXI,UYI,UZI,TXI,TYI,TZI,UXJ,UYJ,UZJ,TXJ,TYJ,TZJ\n')
for beam in ana_model.Beams:
tmp = []
tmp.append(beam.Name)
stress = map(str, beam.OutBeam.Stress)
tmp.extend(stress)
tmp.append('\n')
line = ','.join(tmp)
lines.append(line)
lines.append('\n')
with open(out_file_path, mode='w') as of:
of.writelines(lines)utils.py
便利クラスです。色々な関数をここにまとめて、使いたいところで自由に使えるようにしています。ここでは以下の関数を用意しています。・部材長を計算するために２点間の長さを計算する関数
・全体剛性マトリクスを作るためのマップオン関数
・座標変換するためのマトリクスを取得する関数
# coding:utf-8
import sys, math
sys.path.append('.Model/Analysis/Entity')
from node import Node
import numpy as np
def get_length_between_two_node(nodeI:Node, nodeJ:Node):
"""
２点間の長さを取得する
"""
length_x = abs(nodeI.Coord.X - nodeJ.Coord.X)
length_y = abs(nodeI.Coord.Y - nodeJ.Coord.Y)
length_z = abs(nodeI.Coord.Z - nodeJ.Coord.Z)
length = math.sqrt(length_x * length_x + length_y * length_y + length_z * length_z)
return length
def map_on(dst, row, col, src):
"""
マップオン
"""
for iRow in range(len(src[0])):
for iCol in range(len(src[1])):
dst[row + iRow, col + iCol] += src[iRow][iCol]
return dst
def get_transform_matrix(nodeI:Node, nodeJ:Node):
"""
座標変換マトリクスを取得する
"""
error_value = 1.0E-10
distance_x = nodeJ.Coord.X - nodeI.Coord.X
distance_y = nodeJ.Coord.Y - nodeI.Coord.Y
distance_z = nodeJ.Coord.Z - nodeI.Coord.Z
length = get_length_between_two_node(nodeI, nodeJ)
horz_length = math.sqrt(distance_x * distance_x + distance_y * distance_y)
l = distance_x / length
m = distance_y / length
n = distance_z / length
norm_horz_length = math.sqrt(l * l + m * m)
if horz_length < error_value:
# 直立状態
transMatrix = [ [0.0, 0.0, n],
[ n, 0.0, 0.0],
[0.0, 1.0, 0.0] ]
else:
# 直立以外の状態
transMatrix = [ [ l, m, n],
[ -m / norm_horz_length, l / norm_horz_length, 0.0],
[ -l * n / norm_horz_length, -m * n / norm_horz_length, norm_horz_length] ]
t = np.zeros(shape=(12,12))
map_on(t, 0, 0, transMatrix)
map_on(t, 3, 3, transMatrix)
map_on(t, 6, 6, transMatrix)
map_on(t, 9, 9, transMatrix)
return tviewer.py
結果描画クラスです。描画ライブラリの１つであるMatplotlibを利用した描画処理を記述しています。元の骨組（青線）と変形後の骨組（赤線）を描画しています。# coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
class Viewer:
@staticmethod
def view_frame(beams):
beamsToLine(beams)
def beamToLine(ax, beam):
x0 = beam.NodeI.Coord.X
y0 = beam.NodeI.Coord.Y
z0 = beam.NodeI.Coord.Z
x1 = beam.NodeJ.Coord.X
y1 = beam.NodeJ.Coord.Y
z1 = beam.NodeJ.Coord.Z
ax.plot([x0, x1], [y0, y1], [z0, z1], color='blue', linestyle='solid')
def beamToLine_result(ax, beam):
disp_node_i = beam.NodeI.OutNode.Disp
disp_node_j = beam.NodeJ.OutNode.Disp
x0 = beam.NodeI.Coord.X + disp_node_i[0]
y0 = beam.NodeI.Coord.Y + disp_node_i[1]
z0 = beam.NodeI.Coord.Z + disp_node_i[2]
x1 = beam.NodeJ.Coord.X + disp_node_j[0]
y1 = beam.NodeJ.Coord.Y + disp_node_j[1]
z1 = beam.NodeJ.Coord.Z + disp_node_j[2]
ax.plot([x0, x1], [y0, y1], [z0, z1], color='red', linestyle='dashed')
def beamsToLine(beams):
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
for beam in beams:
beamToLine(ax, beam)
beamToLine_result(ax, beam)
plt.show()解析実行
コマンドプロンプトから以下のように実行します。python main.py解析結果
以下のように、節点変位及び要素応力のCSVファイルと変位図を出力できました。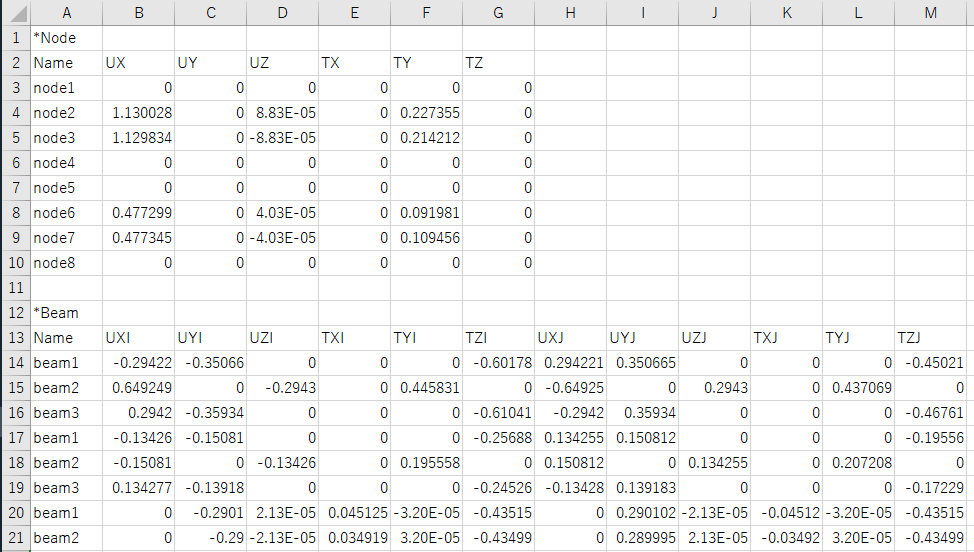
まとめ
今回は立体骨組構造静的弾性解析についてご紹介しました。本記事が構造解析に対する理解の一助になれば幸いです。※本プログラムによるいかなるトラブル、損失、損害について弊社は一切責任を負いません。本記事に掲載している図やプログラムコードはあくまでも一例です。
関連する製品 RESP-F3T
採用情報
構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。 採用HPはこちら→https://www.kke.co.jp/recruit/