【構造解析TIPS】材端剛塑性ばねモデルと適合する RC 部材のファイバーモデル化に関する検討

本記事は2016年度建築学会大会梗概 「材端剛塑性ばねモデルと適合する RC 部材のファイバーモデル化に関する検討」の内容を再編集したものです。

著者：鈴木 壮, 梁川幸盛, 宇佐美祐人, 木村まどか

Keyword：ファイバーモデル, 材端剛塑性ばね, マルチスプリング, RC造, 降伏時剛性低下率

1. はじめに

建築構造設計分野において鉄筋コンクリート柱梁部材は一般的に線材としてモデル化される。また、弾性解析において柱梁部材はTimoshenko梁としてモデル化されることが一般的であるが、曲げに関する弾塑性特性を考慮する場合にはいくつか方法が存在する。代表的なモデル化とその特徴を表1に示す。

表1　梁要素曲げ弾塑性評価手法材端剛塑性ばねモデルは計算負荷が小さいことから一般的によく用いられてきたが、以下の点で課題がある。
1. ひび割れ後の剛性低下を決める際に降伏時軸力を仮定しないとα_yが決定できない。
2. 一軸が基本となるため二軸曲げの影響を考慮することが難しい。
3. 動的解析など繰り返し載荷が生じる場合の除荷剛性の設定や軸力が大きく変動した場合の履歴追跡の根拠づけが難しい。

上記の問題を解決する手法としてMSモデルとファイバーモデルがある。MSモデルとファイバーモデルは断面を分割するという点で似た考え方によるが、最終的に回転ばねとして評価されるか梁要素として評価されるかの違いがある。文献¹⁾でも材端剛塑性ばね、MSモデルにおいては解析モデル上のばね設定が部材の曲げモーメント分布に依存してしまうため、想定と異なるモーメント分布が生じた場合にはモデル化自体不適切な可能性があると指摘している。また、MSモデルとファイバーモデル共通の課題として、材端剛塑性ばねモデルで一般的に用いられる降伏時剛性低下率α_yを表現することが難しいという点が挙げられる。α_yは実験結果から回帰された式であり鉄筋の付着すべりなどの影響が含まれており、これらの影響も適切に考慮する必要がある。しかしながら、付着すべりという現象は平面保持仮定が成立していないため、平面保持仮定を前提としているMSモデルおよびファイバーモデルでは直接的に表現することが難しい。本稿ではファイバーモデルを例にとり、降伏時剛性低下率α_yを表現するためのモデル化について検討を行うことを目的とした。解析には(株)構造計画研究所の「3 次元フレーム汎用解析プログラム RESP-F3T」を用いた。

2. 対象モデル概要

解析対象モデル概要を図1に、断面諸元を図2に示す。境界条件は部材に逆対称モーメントが生じるように両端は回転固定とした。載荷条件は節点2の位置に鉛直力を荷重漸増解析として作用させることとした。モデルは材長3m、6mの2つのモデルについて検討を行った。

図1　解析対象モデル図2　部材断面諸元

3. 材端剛塑性ばねモデルとファイバーモデル比較

解析モデルは M-θ非線形特性を定義した材端剛塑性ばねモデル（以下、M-θ）とファイバーモデルによる比較を行った。M-θ骨格曲線を表2に、Fiber梁要素モデル、分割断面および分割断面の骨格曲線をそれぞれ図3、4、5に示す。なお、Fiberの塑性化領域における非線形特性は端部応力で評価し、塑性化領域内で曲率一定として一律に剛性低下させることとしている。塑性化長さL_pについては道路橋示方書²⁾を参考に以下の式で算出した。

L_p=0.2h−0.1D(0.1D ≤ L_p ≤ 0.5D)

h: 材長, D: 断面せい

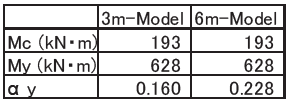
表2　材端剛塑性ばねモデルのM-θ関係図3　Fiber梁要素モデル 

図4　Fiber分割断面 

図5　ファイバー分割断面の骨格曲線結果として今回のモデルでは上限値であるL_p=0.5D としている。また、Fiberについては鉄筋部分をBi-linearとして降伏点のみ考慮したモデル（以下、Fiber）とひび割れを考慮してTri-linearとして考慮したモデル（以下、Fiber-Tri）を検討した。Tri-linearの設定においては下記の仮定を行った。
・第1折点σ_cは曲げ降伏モーメントM_y、曲げひび割れモーメントM_cおよび軸方向降伏応力度σ_yからσ_c=σ_y×(M_c/M_y)として算出した。
・降伏時軸歪みは以下により算出した。（図6参照）
1) 降伏時回転角θ_yから弾性変形分の回転角θ_eを差し引いた塑性回転角θ_pを算出する。
2) 塑性化領域長さL_pにおいてθ_pの回転が生じるときの端部曲率φ_p(=θ_p/L_p）を算出する。
3) 曲げ降伏時の中立軸から引張鉄筋までの距離を7/8dと仮定し、ε_y=φ_p×7/8dとして降伏時歪みを算出する。
4) 第1折点歪みε_c=σ_c/Eで算出し、原点と第 1 折点(ε_c,σ_c)、第 2 折点(ε_y,σ_y) を結ぶ折線により骨格曲線を定義する。算出された応力-歪関係を図7に示す。

図6　Fiber-Tri算出過程 

図7　塑性化領域の応力度-歪関係（左:3mモデル,右:6mモデル）

解析結果比較として曲げモーメント-変位関係を図8に示す。M-θとFiberではひび割れ後の挙動に顕著に差が生じているが、M-θとFiber-Triを比較すると 3m、6mモデルいずれもおおむね近い履歴特性を描いていることが確認できた。

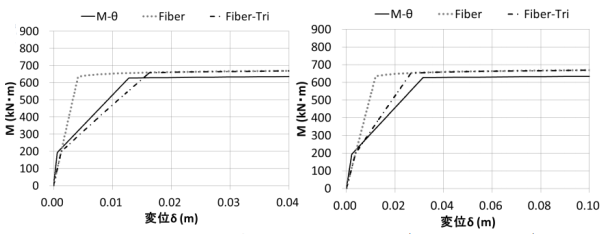図8　モーメント-変位関係（左:3mモデル, 右:6mモデル）

4. まとめ

本検討により得られた知見を以下に示す。
・材端剛塑性ばねモデルによる骨格曲線と適合するファイバーモデルを検討した。
・検討した条件下においては、材端剛塑性ばねモデルによる変形性状とよく一致することが確認できた。

5.課題

今後は以下の課題について調査していく必要がある。
・適切な塑性化領域設定方法の検証
・多様な断面・配筋状況における検証
・軸力変動が生じた際の性状の検証
・モーメント分布が逆対称曲げ以外の場合の検証
・動的な履歴特性に対する検証

参考文献
1) 鉄筋コンクリート構造シンポジウム（その 2）「RC基礎部材と上部構造部材における性能評価の現状と将来」日本建築学会構造委員会鉄筋コンクリート構造運営委員会鉄筋コンクリート部材性能小委員会
2) 「道路橋示方書Ⅴ耐震設計編」公益社団法人日本道路協会
3) 建築省総合技術開発プロジェクト：鉄筋コンクリート造の軽量化・超高層技術の開発, 平成4年度NewRC研究開発概要報告書,国土開発技術センター, 1993.3