OTM低減をおさらいする
ユーザーサポートにおいて、OTM低減に関する問い合わせがありました。 知識として理解していたつもりでも思ったよりもいろいろと忘れていたので、改めてOTM低減とそれを活用する上での注意点おさらいしてみたいと思います。OTMとは?
OTMとは転倒モーメント、Overturning Moment の略です。構造設計者の間ではよく使われる用語です。 計算方法などは簡単に調べられるので、本記事では解説しません。OTM低減をどう使うか?
実際の地震が建物に入力した際、建物に作用する外力は時々刻々変化し、また、正負に繰り返し荷重が作用します。しかしながら、これをそのまま設計用の外力として考慮すると、すべての時刻において部材が健全か判定しなければならず、非常に煩雑です。そのため、従来の設計では地震により発生する最大の層せん断力から設計用外力分布を定め、静的な外力で設計をすることがほとんどです。 時刻歴応答解析から静的設計用外力を定める場合、時刻歴応答解析結果で算出された各層の層せん断力を包絡する形で静的設計用外力を決めます。しかし、時刻歴応答解析では各階の最大層せん断力は同じ時刻には発生しません。つまり、時刻歴応答解析の最大層せん断力を包絡するように設計用せん断力を定めると、本来は同時に作用しないはずの力が同時に作用するという仮定となることで、上層のせん断力の累積として求まる転倒モーメントは過大となります。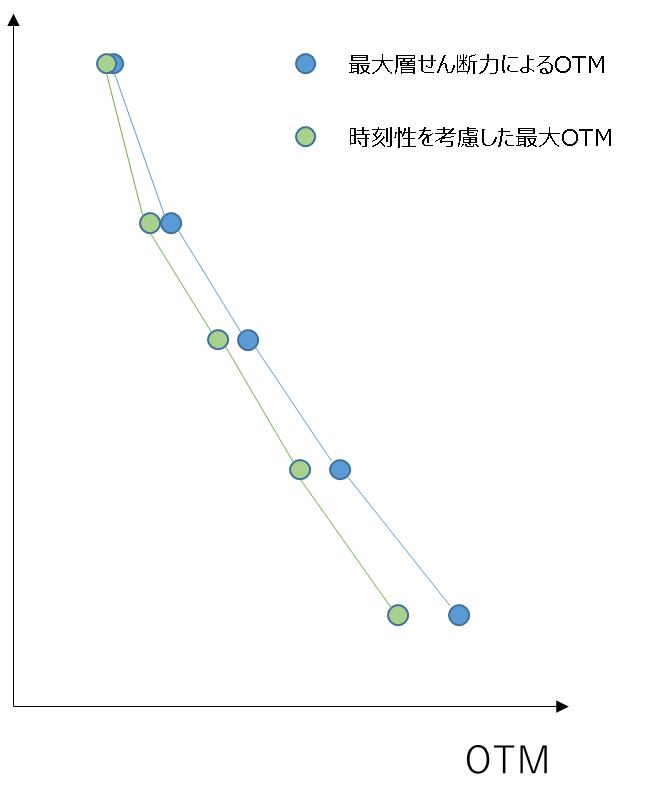
OTM低減の注意点
OTM低減は前述の通り低減係数を用いて外力を低減させることを意味しますが、以下のように水平荷重時に部材に生じる軸力変動を補正する、つまり内力を調整することで考慮されることがよく行われます。$$
N_D=(1.0±C_{UD}) × N_L + C_{OTM} × N_E
$$
$$
N_D : 設計軸力,
N_L : 長期軸力,
N_E : 水平荷重時軸力,
C_{UD} : 上下動軸力係数,
C_{OTM} : OTM低減係数
$$
OTM低減の例
免震支承材の引抜き検討について例を挙げて説明します。 長期面圧が10N/mm^2 の免震支承材を考えます。上下動軸力係数を0.4(4N/mm^2相当)と仮定し、引き抜き側に上下動が作用する仮定を考えると、水平荷重により残り6N/mm^2 以上の引き抜き力が入れば引き抜きに転じることになります。仮に、水平荷重による変動成分が 上下動軸力係数 1.0として10N/mm^2程度だとすると、支承材を弾性と仮定した場合には-4N/mm^2の引き抜きが生じる計算となります。 グラフでは圧縮を正、引張を負として表現しています。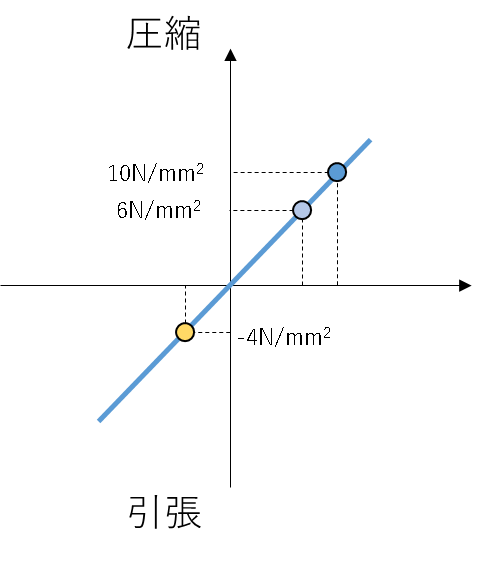
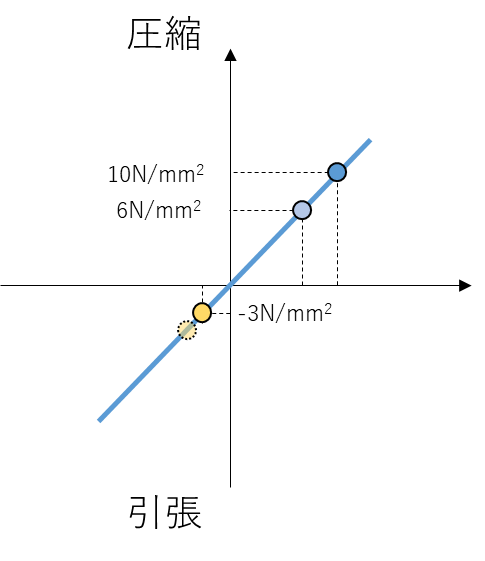
引張側剛性低下率を考慮する場合
支承材を引張側で剛性低下を生じると仮定してみます。仮に、引張非線形を考慮して解析を行った結果、水平荷重による変動分は応力の配分が変わることを考慮し、引張側の応力が1/10になると仮定します。その場合、変動軸力が-6.4N/mm^2 、結果的に-0.4N/mm^2の引抜きになったとします。
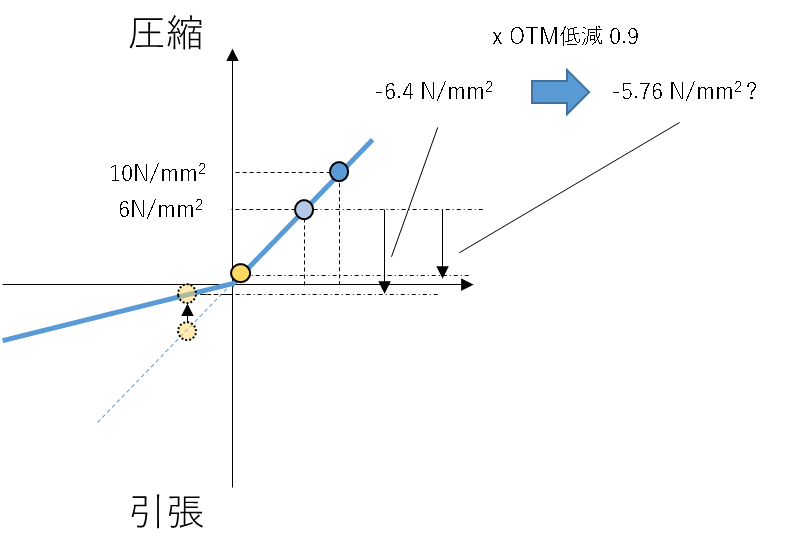
まとめ
OTM低減についてあらためて考えてみました。- OTM低減は、時刻歴応答解析におけるOTMと等価になるように、静的設計用応力を設定するための補正係数である。
- OTM低減は内力に対して補正する方法と、外力を補正する方法がある。
- 弾塑性範囲では、外力を補正しないと適切ではない結果となる可能性がある。