質点系振動解析
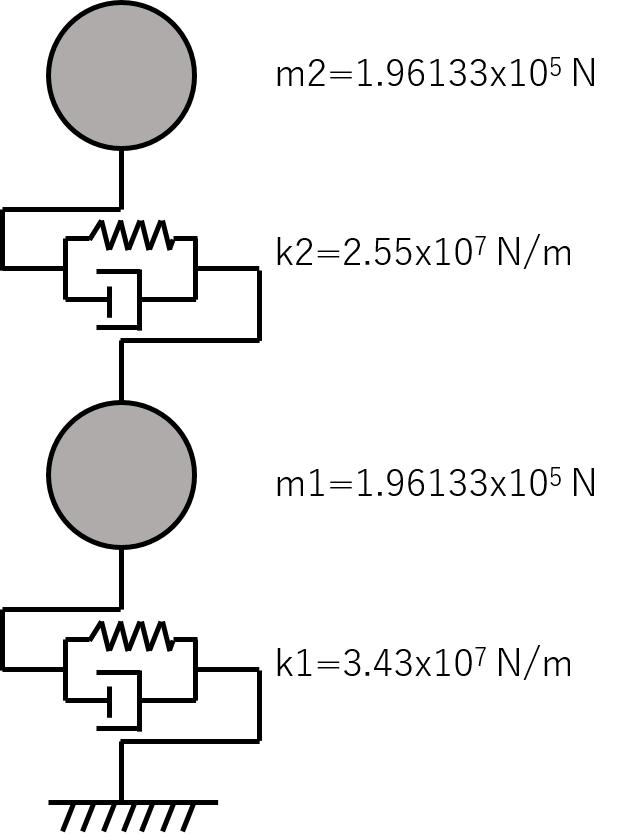
質点系モデルは建物の性状を把握するために良く利用されます。また、以前ご紹介したAMDの検討など、振動解析ベースの検討で簡易に用いることができます。今回は、私が学生の頃にこのような参考にできる記事があったら良かったなあ、という思いで、質点系振動解析プログラムのソースコードを一例としてご紹介します。 ここでは、多質点系モデル(せん断変形のみ考慮)の線形振動解析を対象とします。減衰は初期剛性比例型により考慮します。言語はPython3とします。簡単なサンプル
設定データ
質点系振動解析に関する設定データ(json形式)を用意します。各階の重量や剛性、波形ファイルパスなどを設定します。※「#」以降はコメントです。実際にjsonファイルとして認識させる場合は削除する必要があります。
{
"model": # モデルの設定(重量と剛性)
{
"m":[
196133.0, # 2階重量
196133.0 # 1階重量
],
"k":[
25500000.0, # 2階剛性
34300000.0 # 1階剛性
]
},
"condition": # 計算条件の設定
{
"grav" : 9.80665, # 重力加速度
"dt" : 0.01, # 積分時間刻み
"beta" : 0.25, # Newmarkβ法のβ
"damp_factor" : 0.02, # 減衰定数
"damp_target_period" : 0.26 # 減衰ターゲット周期(剛性比例型)
},
"wave": # 波形の設定
{
"path" : "./samplewave.csv", # 波形ファイルパス
"dt" : 0.02, # 波形時間刻み
"factor": 0.01 # 波形倍率
}
}
出力結果
今回は時刻歴の数値データのみの出力とします。これまでご紹介した記事を参考にすると描画も簡単にできると思います。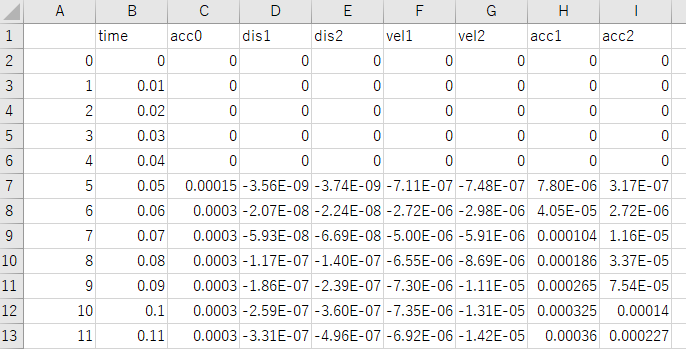
サンプルコード
サンプルコードを以下に示します。Newmarkβ法(*1)を用いて応答計算を実施しています。 *1:柴田明徳(2003)『最新 耐震構造解析 第2版』森北出版株式会社# coding:utf-8
import sys, os, json, math
import numpy as np
import pandas as pd
from docopt import docopt
from scipy import interpolate
# 質点系モデルクラス
class LumpedMassModel:
def __init__(self, size, m_mat, k_mat, c_mat):
self.size = size
self.m = m_mat
self.k = k_mat
self.c = c_mat
# 解析条件クラス
class AnalysisCondition:
def __init__(self, config):
self.grav = float(config['condition']['grav'])
self.dt = float(config['condition']['dt'])
self.beta = float(config['condition']['beta'])
self.damp_factor = float(config['condition']['damp_factor'])
self.damp_target_period = float(config['condition']['damp_target_period'])
# 波形クラス
class Wave:
def __init__(self, config):
self.path = config['wave']['path']
self.dt = float(config['wave']['dt'])
self.factor = float(config['wave']['factor'])
# マップオン
def mapon(part, full, row, col):
row_size = len(part)
col_size = len(part)
for i_row in range(row_size):
for i_col in range(col_size):
target_row = row + i_row
target_col = col + i_col
if 0 <= target_row and 0 <= target_col:
full[target_row][target_col] += part[i_row][i_col]
# 質量マトリクス生成
def build_mass_matrix(m_array, condition):
return np.diag(list(map(lambda x: x / condition.grav, m_array)))
# 剛性マトリクス生成
def build_stiff_matrix(k_array):
size = len(k_array)
full = np.zeros((size, size))
for i in range(size):
k = k_array[i]
part = [[k , -k],
[-k, k]]
mapon(part, full, i-1, i-1)
return full
# 減衰マトリクス生成
def build_damp_matrix(k_mat, factor, period):
omega = 2.0 * math.pi / period
return 2.0 * factor / omega * k_mat
# 初期化
def init(config_file_path):
with open(config_file_path, mode='r') as f:
config = json.load(f)
condition = AnalysisCondition(config)
m_array = config['model']['m']
k_array = config['model']['k']
size = len(m_array)
k_array.reverse() # 下階を上としてマトリクス生成するため
m_array.reverse()
m_mat = build_mass_matrix(m_array, condition)
k_mat = build_stiff_matrix(k_array)
c_mat = build_damp_matrix(k_mat, condition.damp_factor, condition.damp_target_period)
model = LumpedMassModel(size, m_mat, k_mat, c_mat)
wave = Wave(config)
return model, condition, wave
# 固有値解析
def eigen_analysis(model, condition):
lambda_mat = np.linalg.inv(model.m).dot(model.k)
eig_val, eig_vec = np.linalg.eig(lambda_mat)
natural_periods = list(map(lambda omega2: 2.0 * math.pi / math.sqrt(omega2), eig_val))
eigen_vectors = []
for vec in eig_vec:
first_node_vector = vec[-1] # 最下質点の固有ベクトルを1として基準化
eigen_vectors.append(list(map(lambda x: x / first_node_vector, vec)))
df = pd.DataFrame()
df['T'] = sorted(natural_periods, reverse=True) # 固有値は順番がランダムのため、降順で並び替え
df['Vector'] = eigen_vectors
return df
# 波形データ(加速度時刻歴)取得
def get_wave_data(condition, wave):
with open(wave.path, 'r') as f:
df = pd.read_csv(f)
time = df['t'].values.tolist()
acc = list(map(lambda x: x * wave.factor, df['acc'].values.tolist()))
step = int((len(time)-1) * wave.dt / condition.dt)
func_interpolate = interpolate.interp1d(time, acc) # 線形補間関数
new_time = np.arange(0.0, step*condition.dt, condition.dt)
new_acc = func_interpolate(new_time)
return new_acc
# 時刻歴応答解析
def dynamic_analysis(model, condition, wave):
# 初期化
m = model.m
k = model.k
c = model.c
acc0 = get_wave_data(condition, wave)
dt = condition.dt
beta = condition.beta
unit_vector = np.ones(model.size)
pre_acc0 = 0.0
time = 0.0
dis = np.zeros(model.size)
vel = np.zeros(model.size)
acc = np.zeros(model.size)
ddis = np.zeros(model.size)
dvel = np.zeros(model.size)
dacc = np.zeros(model.size)
dis_history = {}
vel_history = {}
acc_history = {}
for i in range(0, model.size):
dis_history[i] = []
vel_history[i] = []
acc_history[i] = []
time_history = []
# Newmarkβ法による数値解析(増分変位による表現)
for i in range(0, len(acc0)):
kbar = k + (1.0/(2.0*beta*dt)) * c + (1.0/(beta*dt**2.0)) * m
dp1 = -1.0 * m.dot(unit_vector) * (acc0[i] - pre_acc0)
dp2 = m.dot((1.0/(beta*dt))*vel + (1.0/(2.0*beta))*acc)
dp3 = c.dot((1.0/(2.0*beta))*vel + (1.0/(4.0*beta)-1.0)*acc*dt)
dp = dp1 + dp2 + dp3
ddis = np.linalg.inv(kbar).dot(dp)
dvel = (1.0/(2.0*beta*dt))*ddis - (1.0/(2.0*beta))*vel - ((1.0/(4.0*beta)-1.0))*acc*dt
dacc = (1.0/(beta*dt**2.0))*ddis - (1.0/(beta*dt))*vel - (1.0/(2.0*beta))*acc
dis += ddis
vel += dvel
acc += dacc
acc_abs = acc + [acc0[i] for n in range(1,model.size)]
[dis_history[i].append(x) for i, x in enumerate(dis)]
[vel_history[i].append(x) for i, x in enumerate(vel)]
[acc_history[i].append(x) for i, x in enumerate(acc_abs)]
time_history.append(time)
time += dt
pre_acc0 = acc0[i]
# 出力オブジェクト
df = pd.DataFrame({'time':time_history,
'acc0':acc0})
for k, v in dis_history.items():
df['dis' + str(k+1)] = v
for k, v in vel_history.items():
df['vel' + str(k+1)] = v
for k, v in acc_history.items():
df['acc' + str(k+1)] = v
return df
# 結果出力
def output(out_file_path, df):
with open(out_file_path, 'w', newline='') as f:
df.to_csv(f)
if __name__ == "__main__":
__doc__ = """
Usage:
main.py <config_file_path> <out_file_dir>
main.py -h | --help
Options:
-h --help show this help message and exit
"""
args = docopt(__doc__)
config_file_path = args['<config_file_path>']
out_file_dir = args['<out_file_dir>']
model, condition, wave = init(config_file_path)
df_eigen = eigen_analysis(model, condition)
df_dyna = dynamic_analysis(model, condition, wave)
os.makedirs(out_file_dir, exist_ok=True)
output(out_file_dir + '/out_eigen.csv', df_eigen)
output(out_file_dir + '/out_dyna.csv', df_dyna)解説
マップオン
一見分かりづらいですが、各層間ばねの剛性マトリクス(要素剛性マトリクス)を全体剛性マトリクスに反映する地道な処理を行っています。引数は、要素剛性マトリクス(part)、全体マトリクス(full)、全体剛性マトリクスに対して要素剛性マトリクスを反映する位置(row, col)としています。固定自由度(自由度番号"-1")に対しては解く必要が無いため、該当する行列部分は除くように剛性マトリクスを作成しています。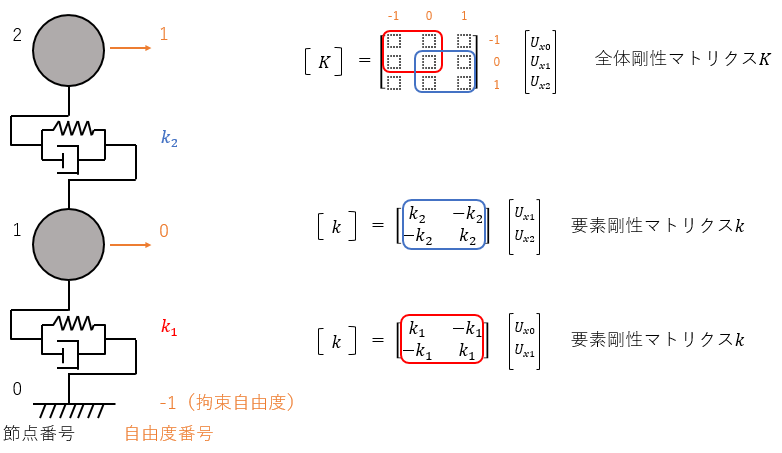
def mapon(part, full, row, col):
row_size = len(part)
col_size = len(part)
for i_row in range(row_size):
for i_col in range(col_size):
target_row = row + i_row
target_col = col + i_col
if 0 <= target_row and 0 <= target_col:
full[target_row][target_col] += part[i_row][i_col]減衰
剛性比例型減衰としています。c=2hk/ωにより減衰マトリクスを生成しています。減衰に関する記事は以下をご参照ください。 【構造解析TIPS】質量比例減衰, 剛性比例減衰, レーリー減衰 【構造解析TIPS】瞬間剛性比例型減衰の種類# 減衰マトリクス生成
def build_damp_matrix(k_mat, factor, period):
omega = 2.0 * math.pi / period
return 2.0 * factor / omega * k_mat応答解析
dynamic_analysis(model, condition, wave)内で実際に応答計算(数値積分)している部分が以下です。入力波形のステップだけループさせています。各ステップで当該ステップの増分応答を求めてそれを前のステップの応答に加算しています。これを毎ステップ繰り返す形で応答計算しています。加速度は出力時には絶対系としていること、各ステップの最後には前ステップの応答を更新する必要があることに注意が必要です。
# Newmarkβ法による数値解析(増分変位による表現)
for i in range(0, len(acc0)):
kbar = k + (1.0/(2.0*beta*dt)) * c + (1.0/(beta*dt**2.0)) * m
dp1 = -1.0 * m.dot(unit_vector) * (acc0[i] - pre_acc0)
dp2 = m.dot((1.0/(beta*dt))*vel + (1.0/(2.0*beta))*acc)
dp3 = c.dot((1.0/(2.0*beta))*vel + (1.0/(4.0*beta)-1.0)*acc*dt)
dp = dp1 + dp2 + dp3
ddis = np.linalg.inv(kbar).dot(dp)
dvel = (1.0/(2.0*beta*dt))*ddis - (1.0/(2.0*beta))*vel - ((1.0/(4.0*beta)-1.0))*acc*dt
dacc = (1.0/(beta*dt**2.0))*ddis - (1.0/(beta*dt))*vel - (1.0/(2.0*beta))*acc
dis += ddis
vel += dvel
acc += dacc
acc_abs = acc + [acc0[i] for n in range(1,model.size)]
[dis_history[i].append(x) for i, x in enumerate(dis)]
[vel_history[i].append(x) for i, x in enumerate(vel)]
[acc_history[i].append(x) for i, x in enumerate(acc_abs)]
time_history.append(time)
time += dt
pre_acc0 = acc0[i]
実行
if __name__ == "__main__":以降が本プログラムのメイン実行部分です。本プログラムはコマンドプロンプトからpython main.py ./config.json ./resultのように実行することで、この部分の処理が行われます。
config_file_path は冒頭でお示しした設定ファイルのパスです。init(config_file_path)でその設定ファイルの内容を解釈して、モデルと計算条件、波形情報を各オブジェクトに設定しています。それらの情報をeigen_analysis(model, condition)やdynamic_analysis(model, condition, wave)のようにメインとなる固有値解析や振動解析を実施する関数に渡しています。それらの関数から返ってきた情報(固有値解析結果(固有周期、固有ベクトル)や振動解析結果(各質点の加速度、速度、変位の時刻歴))をoutput(out_file_dir + 'out_eigen.csv', df_eigen)及びoutput(out_file_dir + 'out_dyna.csv', df_dyna)でファイル出力しています。
if __name__ == "__main__":
__doc__ = """
Usage:
main.py <config_file_path> <out_file_dir>
main.py -h | --help
Options:
-h --help show this help message and exit
"""
args = docopt(__doc__)
config_file_path = args['<config_file_path>']
out_file_dir = args['<out_file_dir>']
model, condition, wave = init(config_file_path)
df_eigen = eigen_analysis(model, condition)
df_dyna = dynamic_analysis(model, condition, wave)
os.makedirs(out_file_dir, exist_ok=True)
output(out_file_dir + '/out_eigen.csv', df_eigen)
output(out_file_dir + '/out_dyna.csv', df_dyna)まとめ
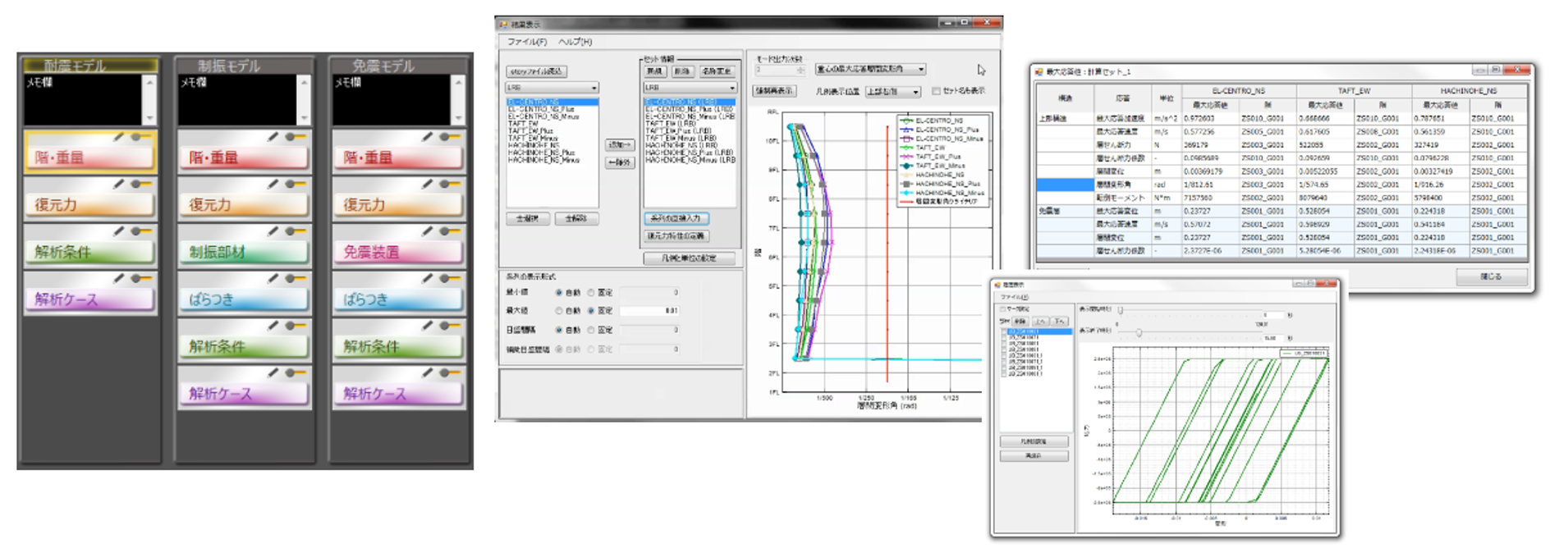
今回は質点系振動解析プログラムのご紹介でした。今回対象としませんでしたが、非線形、曲げ変形、他の減衰パターン、スウェイ・ロッキング、免制振部材などを考慮しようとするともっと複雑になります。自分でこれらを汎用的に使える形でプログラム化することはなかなか大変ですが、RESP-MXは質点系振動解析に特化した汎用的なプログラムとしてご利用いただけます。※本記事で示したプログラムコードによるいかなるトラブル、損失、損害について弊社は一切責任を負いません。本記事に掲載している図やプログラムコードはあくまでも一例です。
RESP-MX
RESP-MXお試し利用は、以下の試供版フォームからお申込みいただけます。採用情報
構造計画研究所 RESPチームでは、いっしょに働いていただけるエンジニアを募集しています。構造設計・構造解析だけでなく、プログラミング技術を活かして新しいものを生み出したいと思っている方、ぜひご応募ください。 採用HPはこちら→https://www.kke.co.jp/recruit/