はじめに
表題の命題は真なのですが、初めは腑に落ちませんでした。
層せん断力-変形曲線(以下、Q-δ曲線)は、固有周期のようにモデル固有の特性で、「微小な刻みで押し切れば、限りなく真に近いQ-δ曲線が得られる」と思っていたからです。
(荷重増分刻みによってもQ-δ曲線の形状は変わりますが、既に記事があるのでここでは議論しません。)
【RESP-D Q&A】荷重増分刻みを変えると荷重増分解析結果が変わるのは何故ですか。
外力分布を変えてQ-δ曲線を書いてみた
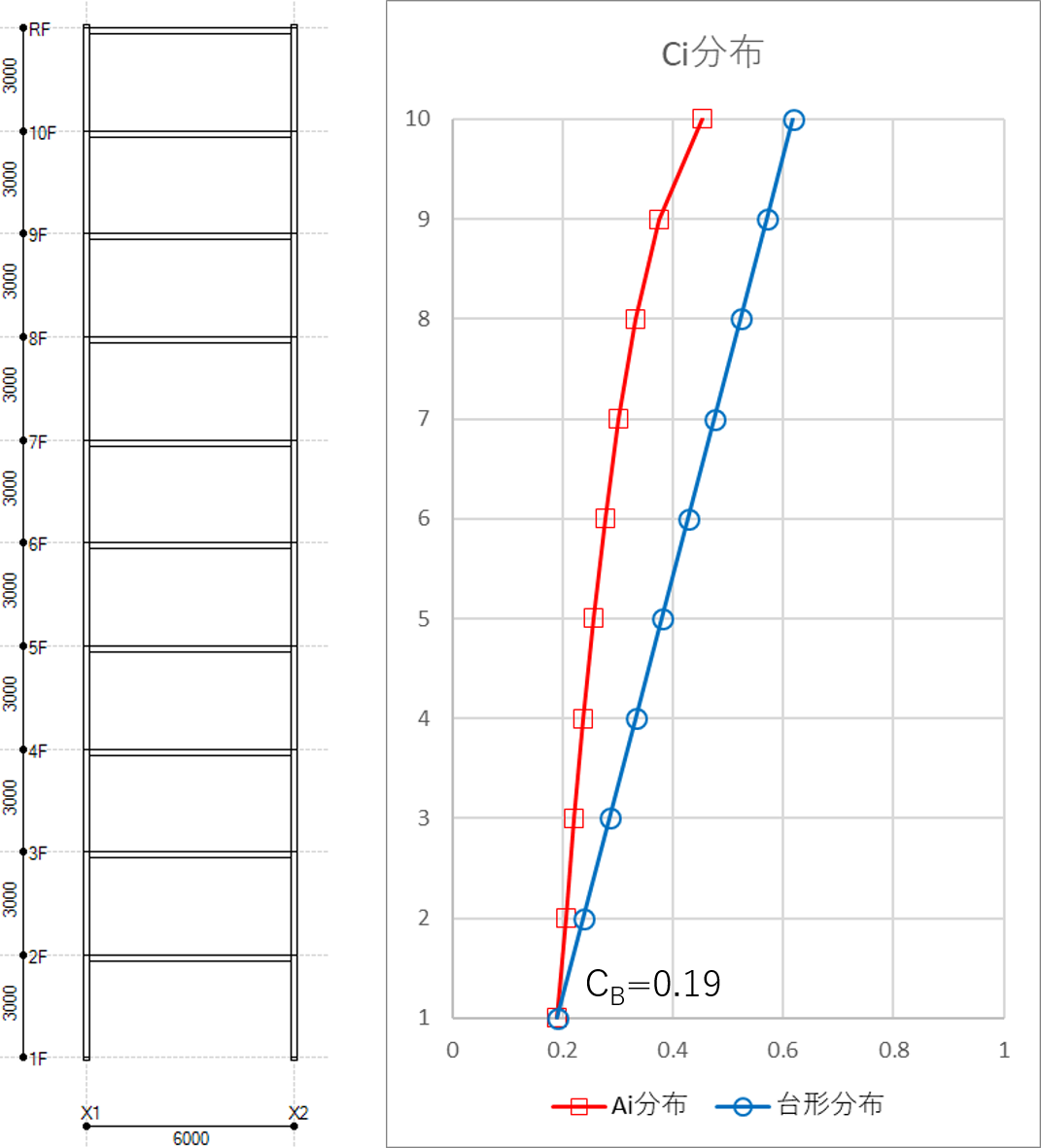
対象とするモデルは、柱脚固定のS造10層1スパンとし、外力分布は以下のようなAi分布と台形分布としました。(※追記:以降すべて台形分布と表記しておりますが、先輩に確認したところ(逆)三角形分布と呼ぶのが一般的だそうです。)
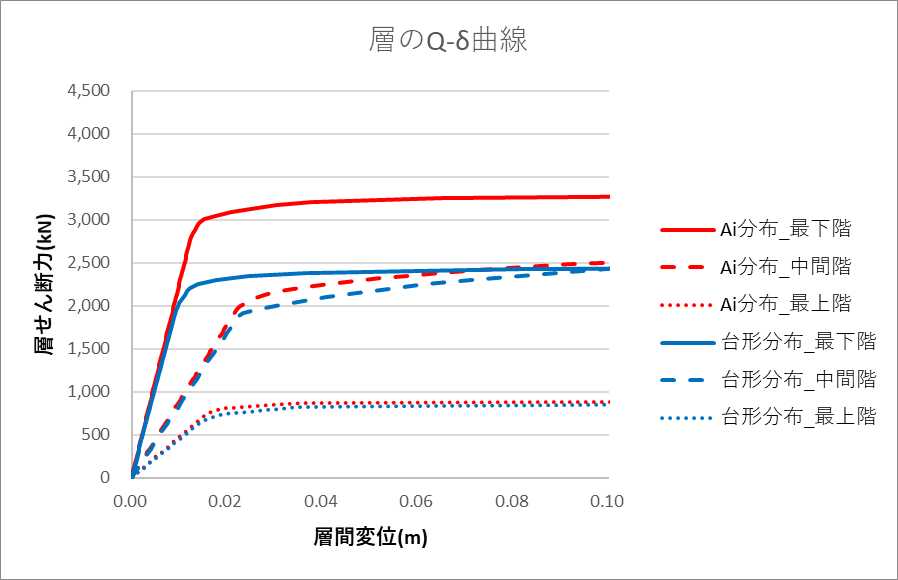
層のQ-δ曲線は以下のようになりました。
なぜ最下階の耐力が大きく変わるのか
層のQ-δ曲線より、最下階の耐力が大きく変わっていますが、これはなぜでしょうか。
最下階に同じ水平力が生じたときのヒンジ図を見てみると以下のようになりました。

外力分布を台形分布で与えた場合には柱脚にヒンジが発生しています。
これは、外力分布を台形分布で与えた場合のほうが建物全体の曲げ変形が支配的となり、柱に生じる軸力が大きくなったため、M-N相関関係より柱脚の曲げ耐力が小さくなったと考えることができます。
一般的な建築物の場合でも、今回のモデルと同様に最下階は柱脚ヒンジの崩壊機構となり、最下階以外は梁ヒンジの崩壊機構となります。
よって、最下階のQ-δ曲線の耐力は柱の軸力変動の影響を受けるため、塔状比の大きい建物では外力分布による影響を受けやすい傾向があると言えます。
一方で、最下階以外のQ-δ曲線の耐力は柱の軸力変動の影響を受けず、結果的に外力分布による影響を受けにくい傾向があると言えます。
また、最下階以外のQ-δ曲線で剛性が急変する点が変わっていますが、これは部材の剛性低下による応力の再分配率が変わったためと考えることができます。
まとめ
Q-δ曲線は、外力分布により以下の影響を受けることがわかりました。
- 一般的に最下階は柱脚ヒンジの崩壊機構となるが、外力分布が変わることにより柱に生じる軸力が変わり、M-N相関関係より柱脚の曲げ耐力が変わり、結果として層せん断耐力が変わる。
- 部材の剛性低下による応力の再分配率が変わるため、最下階以外の骨Q-δ曲線でも剛性が急変する点が変わる。