「本記事は2019年度建築学会大会梗概 「構造設計で利用される履歴モデルの等価減衰定数に関する考察」の内容を再編集したものです」
著者: 梁川 幸盛, 鈴木 壮, 宇佐美 祐人, 木村 まどか
Keyword: 内部粘性減衰, 履歴減衰, 履歴モデル, 武田型, 武藤型
はじめに
近年、免震構造・制振構造の採用によって、大幅に地震時の変形を低減する建築物が増えています。また、BCP(Business Continuity Plan)における地震時損傷推定など、様々な入力レベルの検討が行われるようになってきています。このような検討において利用される履歴モデルは、大変形時のモデル化精度に主眼を置いた古典的なモデルであることが多く、古典的モデルが開発された当時とは異なる変形領域で利用される状況となっています。
本検討では、鉄骨造・鉄筋コンクリート造の時刻歴応答解析で広く用いられている標準型バイリニアおよび剛性逓減型トリリニア(武田型[1])、比較対象として剛性逓減型トリリニア(武藤型[2][3] )について、内部粘性減衰を与え振幅レベルを変化させた時の等価減衰定数の変化を把握し、どのような問題があるのかを考察します。
検討方法
各履歴モデルについて、限界耐力計算の方法に倣い、仮定した塑性率μ に対する等価減衰定数he を式(1)のように求めます。
he = 1 / 4π × ΔW / W ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ ⋯ (1)
ここで、
ΔW :仮定した塑性率を最大変位とする履歴特性曲線で囲まれる面積(図1左)
W :仮定した塑性率により生じる変位に、発生したばね応力を乗じて2で除した値(図1右)
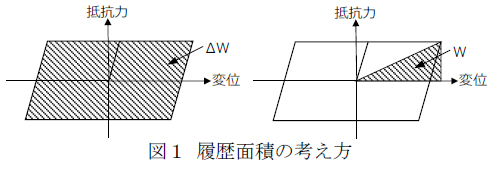
本検討では、履歴面積ΔW を求めるにあたり、正弦波による強制加振を100 サイクル繰り返し、1 サイクル分の平均値を求める方法を用いています。
検討結果(鉄骨造)
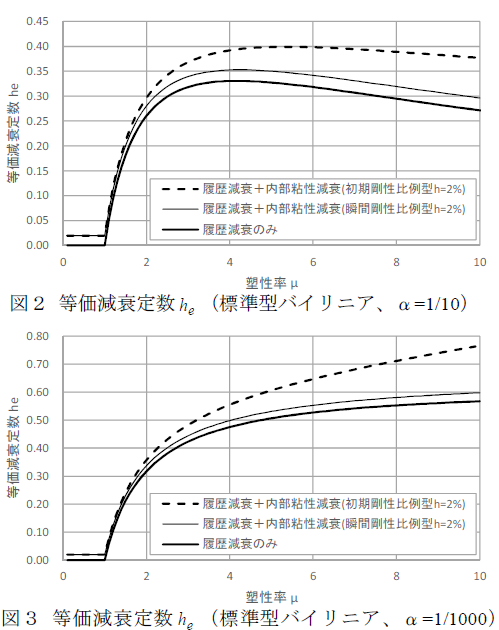
鉄骨造の履歴モデルとして標準型バイリニア(二次勾配と一次勾配の比(α = k2 / k1 = 0.1)、内部粘性減衰定数h = 2%)を対象とし、等価減衰定数he を求めた結果を図2に示します。塑性化が開始する塑性率μ = 1以下では内部粘性減衰として与えたh = 2%が得られ、塑性率μ = 1を超える領域では急激に減衰が高まっています。また、等価減衰定数he は塑性率μ = 4 近辺で頭打ちになり、それ以降はなだらかに低下していくことが分かります。粘性減衰として初期剛性比例型減衰を与えた場合には、塑性率μ が大きくなるにつれて粘性減衰の比率が高まりますが、瞬間剛性比例型減衰の場合には、塑性率 μ に関わらずほぼ一定の等価減衰定数 he となることが見て取れます。
鉄骨造のモデル化において、一般に用いられるα = k2 / k1 = 0.001とした場合の状況を図3に示します。等価減衰定数he の頭打ちは無くなり、単調増加となることが分かります。
検討結果(鉄筋コンクリート造)
鉄筋コンクリート造の履歴モデルとして剛性逓減型トリリニア(武田型)を対象とし、等価減衰定数he を求めた結果を図4に示します。武田型では、塑性率μ = 1以下のひび割れ発生後の領域においてμ = 1時以上の等価減衰定数he が発揮されていることがわかります。また、粘性減衰が占める比率が高く、初期剛性比例型減衰では履歴減衰と合わせて等価減衰定数 he = 10% 近くに達しており、瞬間剛性比例型減衰でも等価減衰定数he = 7% 前後になりました。
武田型の第2勾配における定常履歴ループを図5~6に示します。いずれも平行四辺形の安定履歴を描いています。

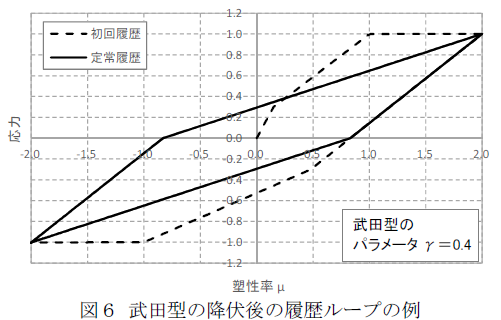
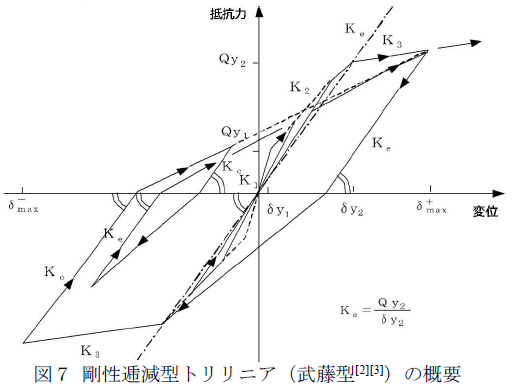
第2勾配上の定常履歴ループにおける過大な履歴減衰が無い剛性逓減型トリリニアとして武藤型[2](学術発表は津川[3]による)について調べた。履歴モデルの概要を図7に示す。本モデルは、第2勾配からの除荷において原点を指向するため、エネルギー消費がほとんど無いことが特徴になります。一方で、本モデルには、武田型の特徴である降伏後の除荷剛性を変位の関数で求めて降伏後の等価減衰を調節する機能(パラメータγによる)はありません。
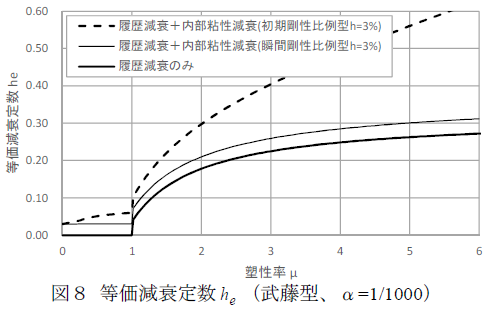
剛性逓減型トリリニア(武藤型)を対象とし、等価減衰定数he を求めた結果を図8に示します。塑性率μ = 1以下のエネルギー吸収は無いが、塑性率μ = 1以上の等価減衰定数he は武田型(γ=0.4)に比べて 5%ポイント程度上昇しました。
まとめ
標準型バイリニアは、塑性率μ の大きな領域で初期剛性比例型減衰が過大となる傾向があることが分かりました。履歴ダンパー等のモデル化では注意する必要があると考えられます。
武田型は、塑性率μ = 1以下で内部粘性減衰と合わせて等価減衰定数he = 7% 前後に達しました。免震・制震での利用では注意する必要があると考えられます。この問題は武藤型にはありませんが、逆に塑性率μ = 1以上での履歴減衰の調節機能がありません。今後は、両者の美点を兼ね備えたモデルを構築するべきだと考えられます。
【謝辞】本検討を行う動機付けは、平石久廣先生(元明治大学教授)、稲井栄一先生(山口大学教授)、北嶋圭二先生(日本大学教授)より示唆された現状の履歴モデルの問題点にありました。ここに記して謝意を表します。
【参考文献】
[1] Takeda, Sozen and Nielsen:Reinforced Concrete Response to Simulated Earthquakes, Journal, Structural Division, ASCE, Vol.96, No.ST12, 1970.
[2] 武藤清, 構造物の動的設計, 丸善, 1977.
[3] 津川恒久, RC 造20 階建てビルのR&D(その5)動的解析, 日本建築学会 大会学術講演梗概集, 1974.