【構造解析TIPS】既往の曲げ降伏時剛性低下率に適合する RC 部材のファイバーモデル化 その1 両端固定梁要素によるパラメトリックスタディ

本記事は2019年度建築学会大会梗概 「既往の曲げ降伏時剛性低下率に適合するRC部材のファイバーモデル化その 1 両端固定梁要素によるパラメトリックスタディ」の内容を再編集したものです

著者：鈴木 壮, 角 友太郎, 宇佐美 祐人, 木村 まどか

Keyword: ファイバーモデル, 材端剛塑性ばね, マルチスプリング, RC造, 降伏時性低下率

1. はじめに
建築構造設計分野において鉄筋コンクリート柱梁部材は一般的に線材としてモデル化され、柱部材に関しては軸力変動を考慮して弾塑性特性が設定される。超高層RCの柱は軸力変動が大きく、2 軸曲げの影響も適切に考慮する必要があるため、それらの影響も精緻に考慮できるファイバーモデルが有用である。
一方、ファイバーモデルでは平面保持仮定が前提であるため、コンクリートの付着すべりの影響などにより平面保持仮定が成立していないような実験結果に対して曲げひび割れ後の剛性が大きく算出される場合がある。既報 ¹⁾ では、実験の回帰式である菅野式²⁾ と近い性状を示すファイバーモデルの構築方法を提案した。本報では設定方法の改良およびより多くの柱断面に対して適用性を確認した。解析には(株)構造計画研究所の「3 次元フレーム汎用解析プログラムRESP-F3T」を用いた。

2. 解析対象モデル概要
解析対象モデル概要を図 1 に、パラメトリックスタディの変動パラメータを表 1 に示す。軸力を初期応力として与え、両端固定の柱に対し水平方向に載荷する。ファイバーモデルにおける塑性化領域 L_p は、柱せい D に対して L_p = 0.5D とし柱頭および柱脚に設け、中間部分は弾性領域とした。図 2 にファイバーモデルにおける鉄筋（トリリニア）、コンクリート（NewRC モデル 3)）の復元力特性を示す。

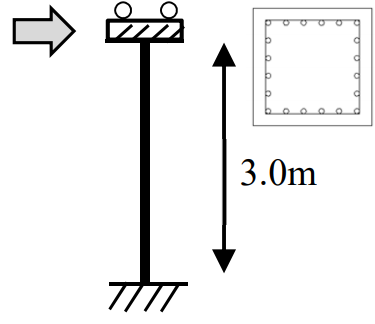
図 1 解析モデル概要

表 1 パラメトリックスタディ変動パラメータ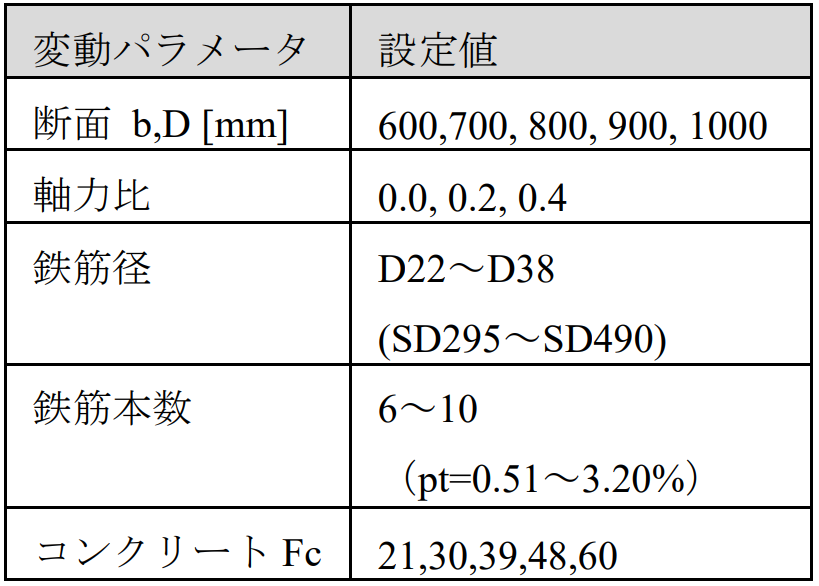

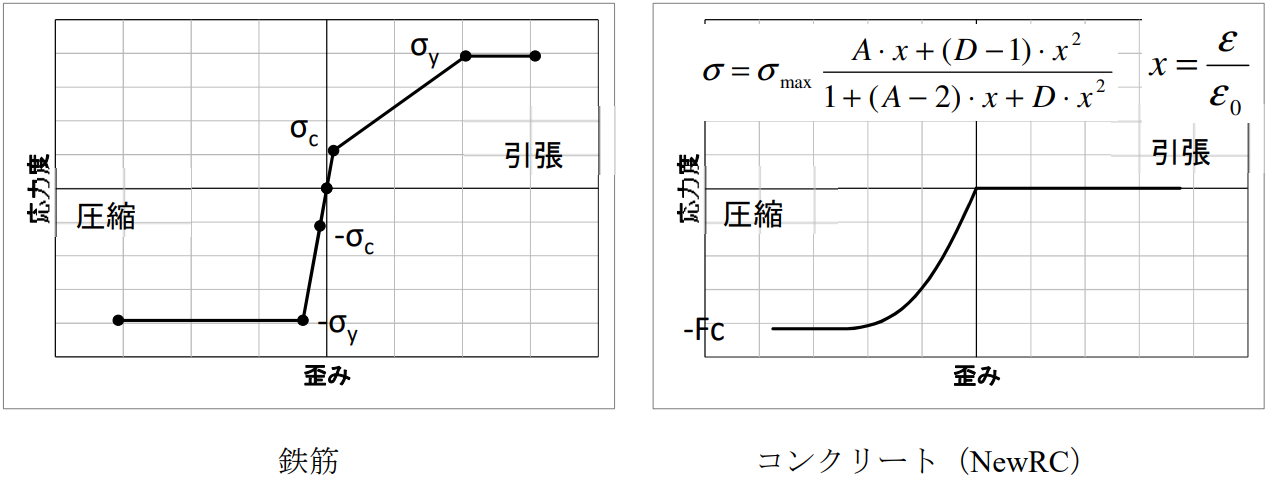
図 2 鉄筋、コンクリートの復元力特性(ファイバー)

3. ファイバーモデルの設定方法
以下に菅野式に適合するファイバーモデル構築のための鉄筋トリリニア復元力特性の設定プロセスを示す。

1）鉄筋第 1 折れ点 σ_c の設定
鉄筋軸方向復元力特性の第 1 折れ点となる σ_c は曲げ降伏モーメント M_y 、曲げひび割れモーメント M_c の比率に比例すると仮定し、軸方向降伏応力度 σ_y から σ_c = σ_y ・ ( M_c / M_y ) として算出する。

2）菅野式による降伏時回転角 θ_y を算出
θ_y = M_y / ( α_y ・ 6EI / L ) から算出する。

3）塑性回転角 θ _p を算出
降伏時回転角 θ_y から部材の塑性化領域を除いた弾性領域の回転角 θ_e を M = ( 6EI / L ) θ_e から算出し、降伏時変形 δ_y とその弾性変形分 δ_e 、塑性変形分 δ_p の関係を δ_y = δ_p + δ_e とする。
ここで、δ_y = θ_y ・ L、δ_p = θ_p ・ L_e 、δ_e = θ_e ・ L_e の関係から、θ_p = ( θ_y ・ L - θ_e ・ L_e ) / L_e として塑性回転角を算出する。

4）端部曲率 φ_p の算出
塑性化領域長さ L_p において θ_p の回転が生じるときの端部曲率 φ_p を以下の θ_p と φ_p の関係から算出する。

 

 

 

 

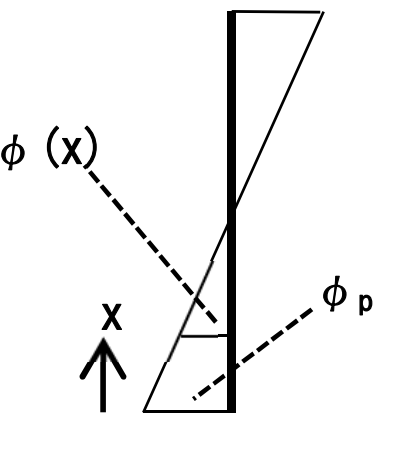
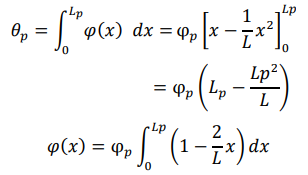
図３ 曲率分布

5）鉄筋の付着を考慮した降伏時歪 ε_y を算出曲げ降伏時の中立軸から引張鉄筋までの距離を 7/8d と仮定し、ε_y = φ_p ・( 7 / 8 ) d として降伏時歪みを算出する。(図 4 参照)

6）鉄筋骨格曲線を設定
ε_c = σ_c / E から算出された ε_c と上記で算出された σ_c,ε_y および σ_y を用いて鉄筋の骨格曲線を設定する。(図 5 参照)

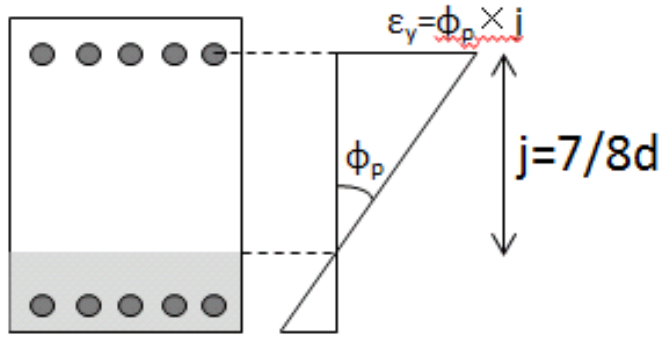
　図４ 曲率と鉄筋歪みの関係　

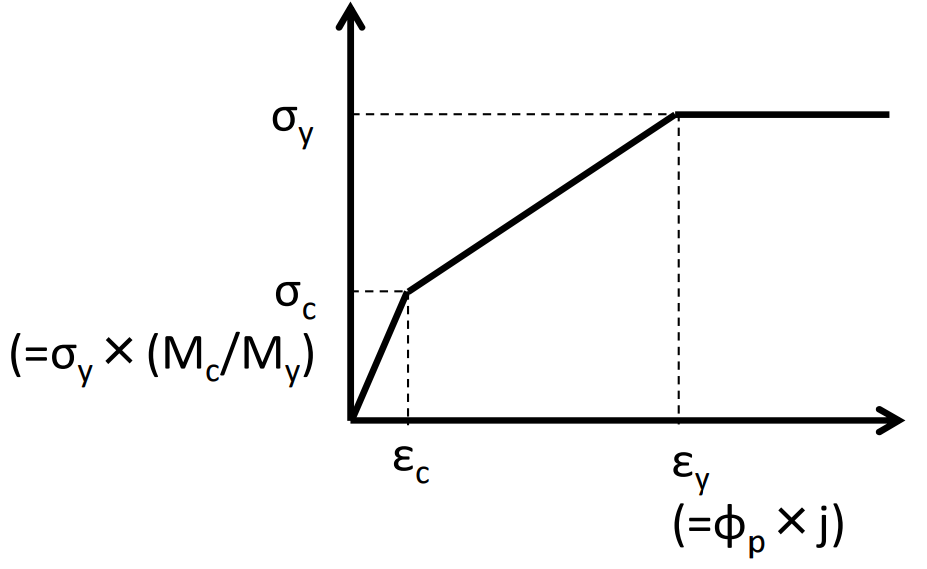　図５ 鉄筋の骨格曲線(引張側)

ここで、M_c,M_y,σ_y は以下の計算式により算出する。

 

 

 

 

M_c : 曲げひび割れ耐力
M_y : 曲げ降伏耐力
F_c : コンクリート圧縮強度
σ_y : 鉄筋強度
Z_e : 断面係数
N : 軸力
b : 柱幅
D : 柱せい
g₁ : jt / D,
a/D : せん断スパン比
η₀ : N / bDσ_B
jt : 引張圧縮鉄筋重心間距離

4. 解析結果
解析結果として、部材の変形角 1/100rad までの履歴エネルギー、曲げ降伏時剛性低下率について既往のトリリニアモデルとファイバーモデルで比較する。既往のトリリニアモデルを M-θ、ファイバーモデルを Fiber と表記する。ファイバーモデルの曲げ降伏時剛性低下率は、文献 ⁴⁾の方法により塑性率基点を算出し、そのステップにおける回転角と曲げモーメントに対する割線勾配から算出した。
結果を図 6 に示す。エネルギー、降伏時回転角の比較は 0.7 倍～1.3 倍の範囲に収まることを確認した。ばらつきの主要な要因としては、曲げ耐力の推定において M-θ では略算式を用いて計算しているのに対し、ファイバーモデルでは断面解析による精算値を用いていることが挙げられる。また、降伏時剛性低下率が既往式に対して 0.7倍～1.3 倍に収まらないケースの多くはa/D<2 のケースとなった。a/D<2 の場合、α_y の計算に p_t の項が含まれないため、その影響により差異が生じたものと考えられる。

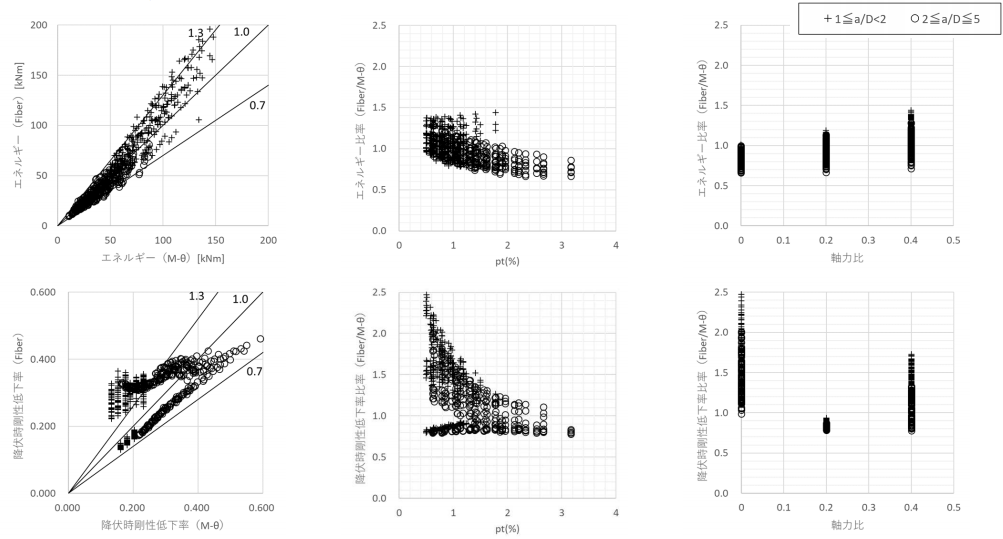
また、p_t が大きくなるとエネルギー、降伏時剛性低下率ともにばらつきが小さくなる傾向が得られた。軸力比については明確な傾向が確認できなかった。
なお、今回の結果はばらつきが大きめであるが、菅野式自体も実験結果に対して 0.7 倍～1.3 倍程度の範囲内に全資料の 90 %が収まる程度の精度であることにも留意する必要がある。

5. まとめ
本検討により得られた知見を以下に示す。
● 既往式に対してより適合したファイバーモデルの構築方法の検証を行い、エネルギーについては 0.7 倍～1.3 倍、降伏時剛性低下率については 2≦a/D であれば 0.7 倍～1.3 倍の範囲におおむね分布することが確認できた。

参考文献
1) 鈴木壮,梁川幸盛ほか「材端剛塑性ばねモデルと適合するRC部材のファイバーモデル化に関する検討」日本建築学会大会学術講演梗概集, 2016
2) 2007 年版　建築物の構造技術基準解説書　全国官報販売協同組合
3) 建築省総合技術開発プロジェクト：鉄筋コンクリート造の軽量化・超高層技術の開発, 平成 4 年度NewRC研究開発概要報告書, 国土開発技術センター, 1993.3
4) 鈴木壮, 會田裕昌ほか「ファイバー要素断面の塑性率算定に関する考察」日本建築学会大会学術講演梗概集, 2013

関連ブログ
【構造解析TIPS】既往の曲げ降伏時剛性低下率に適合する RC 部材のファイバーモデル化 その 2 立体骨組モデルによる確認